Window function

A function used to restrict consideration of an arbitrary function or signal in some way. The terms time-frequency localization, time localization or frequency localization are often used in this context. For instance, the windowed Fourier transform is given by

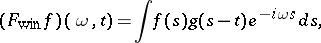where is a suitable window function. Quite often, scaled and translated versions of are considered at the same time, [a1], [a3]. An example is the Gabor transform. (See also Balian–Low theorem; Calderón-type reproducing formula.) Such window functions are also used in numerical analysis.

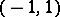More specifically, the phrase window function refers to the function that equals on the interval and zero elsewhere (at and it is arbitrarily defined, usually or ). This function, as well as its scaled and translated versions, is also called the rectangle function or pulse function [a2], pp. 30, 35, 60, 61. However, the phrase "pulse function" is also sometimes used for the delta-function, see also Transfer function.

The Fourier transform of the specific rectangle function (with 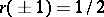) is the function

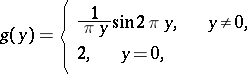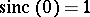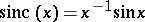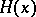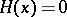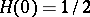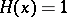a version of the sinc function (, for ), see [a2], pp. 61, 104. In terms of the Heaviside function ( for , , for ), 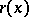is given by

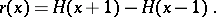There is also a relation with the Dirac delta-function :

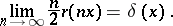References

[a1]	I. Daubechies, "Ten lectures on wavelets" , SIAM (1992) pp. Chap. 1
[a2]	D.C. Champeney, "A handbook of Fourier transforms" , Cambridge Univ. Press (1989)
[a3]	A.I. Saichev, W.A. Woyczyński, "Distributions in the physical and engineering sciences" , 1: Distribution and fractal calculus, integral transforms and wavelets , Birkhäuser (1997) pp. 195ff