Thom spectrum

A spectrum of spaces, equivalent to the spectrum associated to a certain structure series (cf. -structure).

Let be a structure series, and let be the bundle over induced by the mapping . Let be the Thom space of . The mapping induces a mapping , where 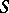is suspension and 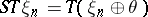( is the one-dimensional trivial bundle). One obtains a spectrum of spaces 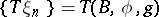, associated with the structure series , and a Thom spectrum is any spectrum that is (homotopy) equivalent to a spectrum of the form 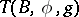. It represents -cobordism theory. Thus, the series of classical Lie groups 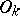, , , and 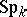lead to the Thom spectra 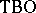, , 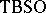, and .

Let 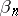be Artin's braid group on strings (cf. Braid theory). The homomorphism , where is the symmetric group, yields a mapping 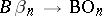such that a structure series arises ( is canonically imbedded in ). The corresponding Thom spectrum is equivalent to the Eilenberg–MacLane spectrum 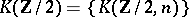, so that is a Thom spectrum (cf. [1], [2]). Analogously, 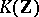is a Thom spectrum, but using sphere bundles, [3].

References

[1]	M. Mahowold, "A new infinite family in 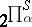" Topology , 16 (1977) pp. 249–256
[2]	S. Priddy, " as a Thom spectrum" Proc. Amer. Math. Soc. , 70 : 2 (1978) pp. 207–208
[3]	M. Mahowold, "Ring spectra which are Thom complexes" Duke Math. J. , 46 : 3 (1979) pp. 549–559