Delange theorem

In 1961 H. Delange (see [a1]) proved that a multiplicative arithmetic function 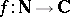of modulus 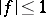possesses a non-zero mean value

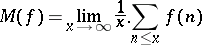if and only if:

i) the Delange series

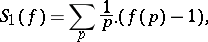extended over the primes, is convergent; and

ii) all the factors 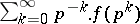of the Euler product of 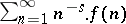are non-zero.

Since 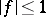, condition ii) is automatically true for every prime . In [a2] this theorem was sharpened.

An elegant proof of the implication "i) and ii) Mf exists" , using the Turán–Kubilius inequality, is due to A. Rényi [a4].

Using the continuity theorem for characteristic functions, for a real-valued additive arithmetic function 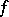Delange's theorem permits one to deal with the problem of the existence of limit distributions .

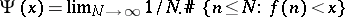Important extensions of Delange's theorem are due to P.D.T.A. Elliott and H. Daboussi; these theorems give necessary and sufficient conditions for multiplicative functions 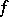with finite semi-norm

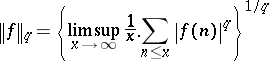to possess a non-zero mean value (respectively, at least one non-zero Fourier coefficient 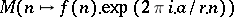). See Elliott–Daboussi theorem. See also Wirsing theorems.

E.V. Novoselov's theory of integration for arithmetic functions (see [a3]) also leads to many results on mean values of arithmetic functions.

References

[a1]	H. Delange, "Sur les fonctions arithmétiques multiplicatives" Ann. Sci. Ecole Norm. Sup. (3) , 78 (1961) pp. 273–304
[a2]	H. Delange, "On a class of multiplicative functions" Scripta Math. , 26 (1963) pp. 121–141
[a3]	E.V. Novoselov, "A new method in probabilistic number theory" Transl. Amer. Math. Soc. , 52 (1966) pp. 217–275 Izv. Akad. Nauk SSSR Ser. Mat. , 28 (1964) pp. 307–364
[a4]	A. Rényi, "A new proof of a theorem of Delange" Publ. Math. Debrecen , 12 (1965) pp. 323–329