Homotopy

of two continuous mappings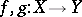

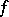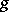A formalization of the intuitive idea of deformability of one mapping into another. More exactly, two mappings and are called homotopic (denoted by 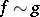) if there exists a family of continuous mappings 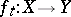, continuously depending on a parameter 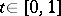, such that 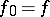, 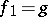(the choice of the segment 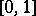is here only for the sake of technical convenience; it is clear that any other segment of the real axis could have been taken just as well). This family (which is known as a homotopy connecting 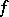with 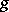) is a path in the space 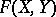of all continuous mappings connecting the point 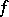with the point 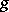. Thus, a homotopy of mappings is a specialization to the space of mappings of the general concept of "being connected by a continuous path" . Thus, in particular, the homotopy relation is an equivalence relation, whose equivalence classes (homotopy classes) are the path-connected components of 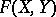. In order to give an exact meaning to the above-said one must specify the meaning of the expression "the mappings ft continuously depend on t" . The most natural procedure is to introduce a topology (or at least a pseudo-topology, cf. also Topological structure (topology)) in 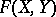. However, the traditional procedure is different — it is assumed, by definition, that the 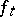continuously depend on 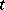if the function 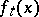is continuous with respect to the totality of variables, i.e. if the mapping 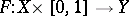defined by the formula 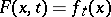is continuous (this mapping is in fact often referred to as a homotopy connecting 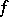with ).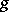

This description of a homotopy is sometimes qualified as free, in distinction from "relative homotopyrelative" or "bound homotopybound" homotopies, which arise upon fixing a class 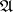of continuous mappings , by imposing the requirement for any 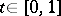. Thus, given a subspace 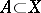it is possible to consider relative homotopies on 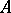, distinguished by the fact that 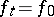on 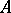for all 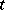. One says in this case that the mapping 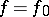is homotopic with the mapping 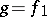relative to ; this is written as .

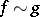
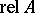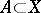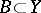Another type of "relative" homotopies is generated by selecting subspaces and in 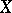and 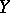and by considering only mappings 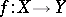that satisfy the condition . Such mappings are called mappings of the pair 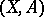into the pair (written as 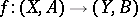), while the corresponding homotopies (i.e. the homotopies for which 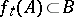for all ) are known as homotopies of pair mappings. Triplets 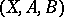(with the condition or without it), quadruplets, etc., rather than pairs, can also be considered. Thus, one can consider homotopy of pair mappings relative to a third subspace, etc. Essentially different types of "relative" homotopies may also be considered.

The task of establishing homotopy ( "relative" or not) of two given mappings 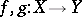is equivalent to the task of extending to 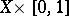a continuous mapping into 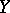given on 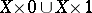(and, in a homotopy problem , on 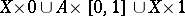). In this sense, the problem of homotopy is a special case of the problem of extension. In a wide class of individual cases, however (viz. for the so-called cofibrations, cf. Cofibration), the possibility of extending to 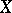a continuous mapping 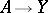given on a subspace 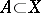depends only on its homotopy class. This close connection between the problem of homotopy and the problem of extension is the reason why they are considered together under the heading of so-called homotopy theory. See Homotopy type.

Comments

The context in which the term "free homotopy" is used differs slightly in the West; one uses it in the context of pointed spaces (a pointed space is a pair 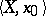with 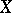a space and 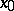a point of 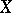). Here then a "free" homotopy is a homotopy between arbitrary mappings, whereas for an "ordinary" homotopy one considers mappings 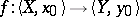satisfying 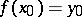and the mappings in the homotopies are to satisfy this condition too.

References

[a1]	G.W. Whitehead, "Elements of homotopy theory" , Springer (1978) pp. 228