Universal series
A series of functions
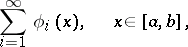 | (1) |
by means of which all functions of a given class can be represented in some way or other. For example, there exists a series (1) such that every continuous function 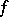 on
on 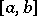 can be approximated by partial sums of this series,
can be approximated by partial sums of this series, 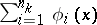 , converging uniformly to
, converging uniformly to 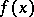 on
on 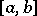 .
.
There exist trigonometric series
 | (2) |
with coefficients tending to zero, such that every (Lebesgue-) measurable function 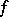 on
on 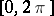 has an approximation by partial sums of the series (2), converging to
has an approximation by partial sums of the series (2), converging to 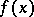 almost everywhere.
almost everywhere.
The given series is called universal relative to approximation by partial sums. One may consider other definitions of universal series. For example, series (1) which are universal relative to subseries 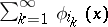 or relative to permutations of the terms of (1).
or relative to permutations of the terms of (1).
References
| [1] | G. Alexits, "Convergence problems of orthogonal series" , Pergamon (1961) (Translated from German) |
| [2] | N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian) |
| [3] | A.A. Talalyan, "The representation of measurable functions by series" Russian Math. Surveys , 15 : 5 (1960) pp. 75–136 Uspekhi Mat. Nauk , 15 : 5 (1960) pp. 77–141 |
Universal series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Universal_series&oldid=18101