Matrix variate distribution
A matrix random phenomenon is an observable phenomenon that can be represented in matrix form and that, under repeated observations, yields different outcomes which are not deterministically predictable. Instead, the outcomes obey certain conditions of statistical regularity. The set of descriptions of all possible outcomes that may occur on observing a matrix random phenomenon is the sampling space 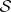 . A matrix event is a subset of
. A matrix event is a subset of 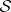 . A measure of the degree of certainty with which a given matrix event will occur when observing a matrix random phenomenon can be found by defining a probability function on subsets of
. A measure of the degree of certainty with which a given matrix event will occur when observing a matrix random phenomenon can be found by defining a probability function on subsets of 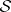 , assigning a probability to every matrix event.
, assigning a probability to every matrix event.
A matrix 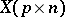 consisting of
consisting of  elements
elements 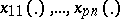 which are real-valued functions defined on
which are real-valued functions defined on 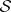 is a real random matrix if the range
is a real random matrix if the range 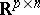 of
of
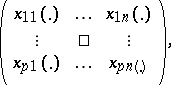 |
consists of Borel sets in the 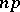 -dimensional real space and if for each Borel set
-dimensional real space and if for each Borel set 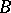 of real
of real  -tuples, arranged in a matrix,
-tuples, arranged in a matrix,
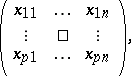 |
in 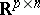 , the set
, the set
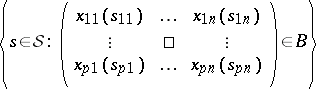 |
is an event in  . The probability density function of
. The probability density function of  (cf. also Density of a probability distribution) is a scalar function
(cf. also Density of a probability distribution) is a scalar function 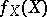 such that:
such that:
i) 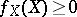 ;
;
ii) 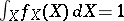 ; and
; and
iii) 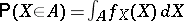 , where
, where  is a subset of the space of realizations of
is a subset of the space of realizations of 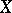 . A scalar function
. A scalar function 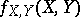 defines the joint (bi-matrix variate) probability density function of
defines the joint (bi-matrix variate) probability density function of 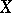 and
and 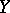 if
if
a) 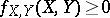 ;
;
b) 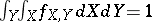 ; and
; and
c) 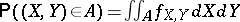 , where
, where 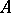 is a subset of the space of realizations of
is a subset of the space of realizations of  .
.
The marginal probability density function of 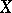 is defined by
is defined by 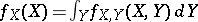 , and the conditional probability density function of
, and the conditional probability density function of 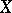 given
given 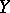 is defined by
is defined by
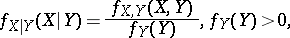 |
where 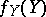 is the marginal probability density function of
is the marginal probability density function of 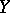 .
.
Two random matrices 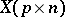 and
and 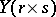 are independently distributed if and only if
are independently distributed if and only if
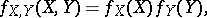 |
where 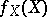 and
and 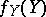 are the marginal densities of
are the marginal densities of 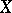 and
and 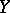 , respectively.
, respectively.
The characteristic function of the random matrix  is defined as
is defined as
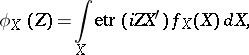 |
where 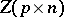 is a real arbitrary matrix and
is a real arbitrary matrix and 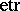 is the exponential trace function
is the exponential trace function 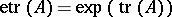 .
.
For the random matrix 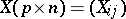 , the mean matrix is given by
, the mean matrix is given by 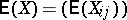 . The
. The 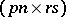 covariance matrix of the random matrices
covariance matrix of the random matrices 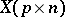 and
and 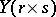 is defined by
is defined by
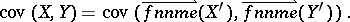 |
Examples of matrix variate distributions.
The matrix variate normal distribution
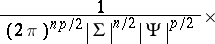 |
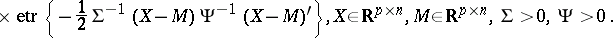 |
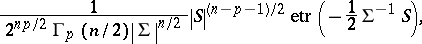 |
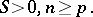 |
The matrix variate 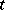 -distribution
-distribution
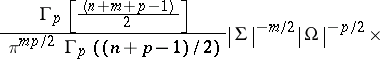 |
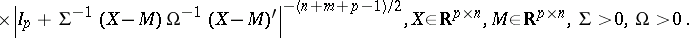 |
The matrix variate beta-type-I distribution
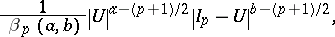 |
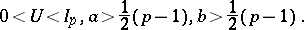 |
The matrix variate beta-type-II distribution
 |
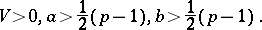 |
References
| [a1] | P. Bougerol, J. Lacroix, "Products of random matrices with applications to Schrödinger operators" , Birkhäuser (1985) |
| [a2] | M. Carmeli, "Statistical theory and random matrices" , M. Dekker (1983) |
| [a3] | "Random matrices and their applications" J.E. Cohen (ed.) H. Kesten (ed.) C.M. Newman (ed.) , Amer. Math. Soc. (1986) |
| [a4] | A.K. Gupta, T. Varga, "Elliptically contoured models in statistics" , Kluwer Acad. Publ. (1993) |
| [a5] | A.K. Gupta, V.L. Girko, "Multidimensional statistical analysis and theory of random matrices" , VSP (1996) |
| [a6] | M.L. Mehta, "Random matrices" , Acad. Press (1991) (Edition: Second) |
Matrix variate distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Matrix_variate_distribution&oldid=18096