Henselization of a valued field

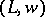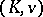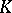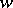A minimal algebraic extension of a valued field (i.e., a field equipped with a valuation ) such that the valuation ring of satisfies the Hensel lemma. This holds if and only if admits a unique extension to every algebraic extension field of 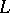(cf. [a2]). Therefore, Henselizations can be characterized as the decomposition fields of the extensions 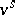of to the separable-algebraic closure 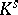of 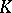(see Ramification theory of valued fields). The minimality is expressed by the following universal property of Henselizations: they admit a unique embedding over in every other Henselian extension field of 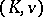(cf. [a2]). In particular, the Henselization of 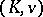is unique up to a valuation-preserving isomorphism over 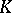; thus, it makes sense to denote it by 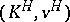(there are some other notations in the literature). The extension 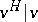is immediate (see also valuation); for an elegant proof, see [a1].

References

[a1]	J. Ax, "A metamathematical approach to some problems in number theory, Appendix" D.J. Lewis (ed.) , Proc. Symp. Pure Math. , 20 , Amer. Math. Soc. (1971) pp. 161–190
[a2]	P. Ribenboim, "Théorie des valuations" , Presses Univ. Montréal (1964)