Mackey intertwining number theorem
intertwining number theorem.
Let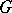 
be a finite group. The intertwining number between two representations 
, 
, is, by definition, the dimension of the space of 
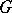-homomorphisms 
: 
.
Now let 
be subgroups of 
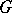, and 
a 
double coset in 
(i.e.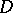 
is a set of the form 
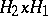for some 
). Let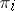 
be a unitary representation of 
and let 
be the corresponding induced representation of 
, 
. Consider the intertwining number between the unitary representations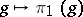 
and 
of the subgroup 
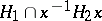for some 
. Then this number only depends on 
(and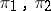 
). It is denoted by 
.
For the intertwining number between the induced representations 
of 
, 
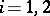, one now has the intertwining number formula
 |
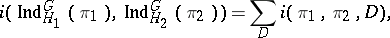where the sum is over the set of all 
double cosets.
The Frobenius reciprocity theorem 
(cf. Induced representation) for representations 
of 
and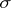 
of a subgroup 
of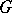 
is an immediate consequence.
For a discussion of the intertwining number theorem for locally compact groups cf. [a2].
References
| [a1] | C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962) pp. §44 |
| [a2] | G. Warner, "Harmonic analysis on semi-simple Lie groups" , 1 , Springer (1972) pp. Chapt. V |
Mackey intertwining number theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mackey_intertwining_number_theorem&oldid=17864