Two-dimensional annulus
in topology
A topological image of the closed part of the plane comprised between two non-identical concentric circles. A two-dimensional annulus is an orientable two-dimensional manifold of genus zero with two boundary components.
Comments
Thus, a  -dimensional annulus is homeomorphic to
-dimensional annulus is homeomorphic to 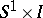 , where
, where 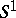 is the circle and
is the circle and 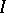 the interval. An
the interval. An  -dimensional annulus is a space homeomorphic to
-dimensional annulus is a space homeomorphic to  . The
. The  -dimensional annulus conjecture states that for any homeomorphism
-dimensional annulus conjecture states that for any homeomorphism  such that
such that 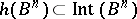 , the interior of
, the interior of 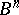 , the closed difference
, the closed difference
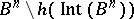 |
is homeomorphic to the annulus 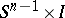 . Here,
. Here, 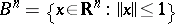 .
.
The stable homeomorphism conjecture asserts that any orientation-preserving homeomorphism 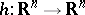 can be written as a finite product,
can be written as a finite product, 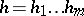 , where each
, where each 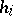 is the identity on some open subset of
is the identity on some open subset of 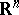 .
.
The stable homeomorphism conjecture for dimension  implies the annulus conjecture for dimension
implies the annulus conjecture for dimension  .
.
The stable homeomorphism conjecture (and hence the annulus conjecture) has finally been established for all  :
: 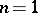 , classical;
, classical; 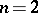 , [a6];
, [a6]; 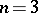 , ;
, ; 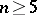 , [a3]; and, finally,
, [a3]; and, finally, 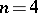 , [a2], as an application of a special controlled
, [a2], as an application of a special controlled 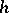 -cobordism theorem in dimension
-cobordism theorem in dimension  , called the thin
, called the thin 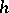 -cobordism theorem or Quinn's thin
-cobordism theorem or Quinn's thin 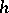 -cobordism theorem.
-cobordism theorem.
References
| [a1] | R.D. Edwards, "The solution of the 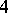 -dimensional annulus conjecture (after Frank Quinn)" Contemporary Math. , 35 (1984) pp. 211–264 -dimensional annulus conjecture (after Frank Quinn)" Contemporary Math. , 35 (1984) pp. 211–264 |
| [a2] | F. Quinn, "Ends of maps III: dimensions 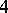 and and  " J. Diff. Geom. , 17 (1982) pp. 503–521 " J. Diff. Geom. , 17 (1982) pp. 503–521 |
| [a3] | R. Kirby, "Stable homeomorphisms and the annulus conjecture" Ann. of Math. , 89 (1969) pp. 575–582 |
| [a4a] | E.E. Moise, "Affine structures in  -manifolds I" Ann. of Math. , 54 (1951) pp. 506–533 -manifolds I" Ann. of Math. , 54 (1951) pp. 506–533 |
| [a4b] | E.E. Moise, "Affine structures in  -manifolds II, III" Ann. of Math. , 55 (1952) pp. 172–176; 203–222 -manifolds II, III" Ann. of Math. , 55 (1952) pp. 172–176; 203–222 |
| [a4c] | E.E. Moise, "Affine structures in  -manifolds IV" Ann. of Math. , 56 (1952) pp. 96–114 -manifolds IV" Ann. of Math. , 56 (1952) pp. 96–114 |
| [a5] | M. Brown, H. Gluck, "Stable structures on manifolds I-III" Ann. of Math. , 79 (1974) pp. 1–58 |
| [a6] | T. Radó, "Über den Begriff der Riemannsche Fläche" Acta Univ. Szeged , 2 (1924–1926) pp. 101–121 |
Two-dimensional annulus. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Two-dimensional_annulus&oldid=17821