Mean-square approximation of a function

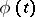An approximation of a function by a function , where the error measure 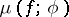is defined by the formula

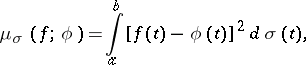where 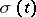is a non-decreasing function on 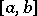different from a constant.

Let

(*)

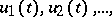be an orthonormal system of functions on 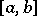relative to the distribution 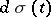. In the case of a mean-square approximation of the function 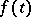by linear combinations 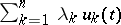, the minimal error for every 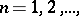is given by the sums

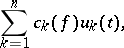where 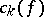are the Fourier coefficients of the function 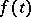with respect to the system (*); hence, the best method of approximation is linear.

References

[1]	V.L. Goncharov, "The theory of interpolation and approximation of functions" , Moscow (1954) (In Russian)
[2]	G. Szegö, "Orthogonal polynomials" , Amer. Math. Soc. (1975)

Comments

Cf. also Approximation in the mean; Approximation of functions; Approximation of functions, linear methods; Best approximation; Best approximation in the mean; Best linear method.

References

[a1]	E.W. Cheney, "Introduction to approximation theory" , McGraw-Hill (1966) pp. Chapts. 4&6
[a2]	I.P. Natanson, "Constructive theory of functions" , 1–2 , F. Ungar (1964–1965) (Translated from Russian)