Closed monoidal category
A category 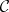 is monoidal if it consists of the following data:
is monoidal if it consists of the following data:
1) a category 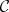 ;
;
2) a bifunctor 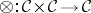 ;
;
3) an object 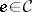 ; and
; and
4) three natural isomorphisms 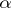 ,
, 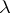 ,
,  such that
such that
A1) 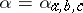 :
: 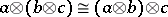 is natural for all
is natural for all 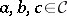 and the diagram
and the diagram
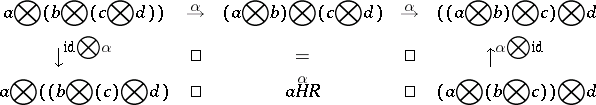 |
commutes for all  ;
;
A2) 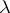 and
and 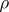 are natural and
are natural and  :
: 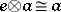 ,
, 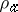 :
: 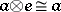 for all objects
for all objects 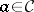 and the diagram
and the diagram
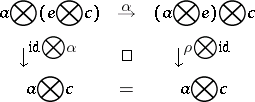 |
commutes for all  ;
;
A3)  :
: 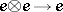 .
.
These axioms imply that all such diagrams commute.
Some examples of monoidal categories are:
E1) any category with finite products is monoidal if one takes 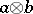 to be the (chosen) product of the objects
to be the (chosen) product of the objects  and
and 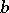 , with
, with  the terminal object;
the terminal object; 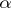 ,
, 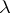 and
and 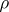 are the unique isomorphisms that commute with the appropriate projections;
are the unique isomorphisms that commute with the appropriate projections;
E2) the usual "tensor products" give monoidal categories — whence the notation. Note that one cannot identify all isomorphic objects in 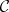 .
.
Closed categories.
A monoidal category 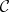 is said to be symmetric if it comes with isomorphisms
is said to be symmetric if it comes with isomorphisms 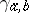 :
:  natural on
natural on 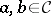 such that the following diagrams all commute:
such that the following diagrams all commute:
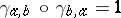 ,
, 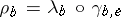 :
:  :
:
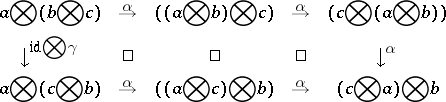 |
A closed category  is a symmetric monoidal category in which each functor
is a symmetric monoidal category in which each functor  has a specified right-adjoint
has a specified right-adjoint 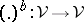 .
.
Some examples of closed monoidal categories are:
E3) the category 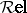 of relations, whose objects are sets
of relations, whose objects are sets  and in which an arrow
and in which an arrow 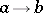 is a subset
is a subset 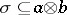 ; the object
; the object 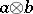 is the Cartesian product of the two sets, which is not the product in this category;
is the Cartesian product of the two sets, which is not the product in this category;
E4) the subsets of a monoid 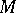 (a poset, hence a category); if
(a poset, hence a category); if 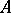 ,
, 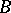 are two subsets of
are two subsets of 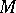 , then
, then 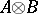 is
is  while
while 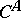 is
is 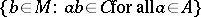 .
.
References
| [a1] | M. Barr, C. Wells, "Category theory for computing science" , CRM (1990) |
| [a2] | S. MacLane, "Categories for the working mathematician" , Springer (1971) |
Closed monoidal category. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Closed_monoidal_category&oldid=17458