Contraction of a representation
onto an invariant subspace
The contraction of a representation  of a group
of a group  onto a subgroup
onto a subgroup  (of an algebra
(of an algebra  onto a subalgebra
onto a subalgebra  ) is the representation
) is the representation  of the group (algebra)
of the group (algebra)  defined by the formula
defined by the formula  for all
for all  . A contraction of a representation
. A contraction of a representation 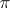 is also called a restriction (or reduction) of the representation
is also called a restriction (or reduction) of the representation 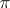 onto an invariant subspace or onto a subgroup or subalgebra. If
onto an invariant subspace or onto a subgroup or subalgebra. If 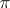 is a continuous representation, then a contraction of
is a continuous representation, then a contraction of 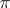 is also continuous.
is also continuous.
Comments
More usually one speaks of restriction of a representation and reduction of a representation. More precisely, if  is a representation of a group, algebra
is a representation of a group, algebra and
and 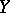 is a subgroup, subalgebra
is a subgroup, subalgebra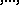 then
then 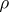 can be restricted to
can be restricted to 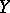 . Secondly, if
. Secondly, if  is an invariant subspace of
is an invariant subspace of  , then
, then  induces a representation of
induces a representation of  (and
(and  ) in
) in 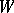 yielding a subrepresentation of the given representation; this is sometimes called reduction of a representation to an invariant subspace. The phrase contraction of a representation refers more often to the following situation. Consider a representation
yielding a subrepresentation of the given representation; this is sometimes called reduction of a representation to an invariant subspace. The phrase contraction of a representation refers more often to the following situation. Consider a representation 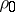 over a ring
over a ring  of an algebra
of an algebra  (or group) in an
(or group) in an  -module
-module  ,
,  . Suppose that there is a representation
. Suppose that there is a representation  of
of 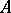 over
over  ,
, 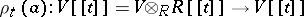 such that
such that 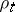
 (i.e.
(i.e. 
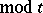 for all
for all  ). Here
). Here 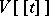 denotes the module of power series in
denotes the module of power series in 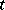 with coefficients in
with coefficients in  . Then the representation
. Then the representation  is said to be a contraction of
is said to be a contraction of  and
and  is called a deformation of
is called a deformation of 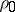 . Intuitively
. Intuitively  is an (infinitesimal) family of representations parametrized by
is an (infinitesimal) family of representations parametrized by 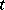 . More generally one also considers the situation where the algebra
. More generally one also considers the situation where the algebra 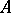 is also deformed at the same time, so that one has an algebra
is also deformed at the same time, so that one has an algebra  over
over 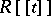 such that
such that 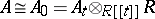 and a representation
and a representation  of
of  over
over  . Cf. also Deformation.
. Cf. also Deformation.
Contraction of a representation. A.I. Shtern (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Contraction_of_a_representation&oldid=17456