Jet
From Encyclopedia of Mathematics
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
A polynomial 
obtained by the truncation of the (formal) Taylor series of a differentiable function 
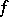. More precisely, let 
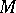and 
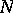be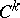 
-manifolds. The class 
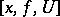of equivalent triples 
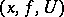, where 
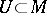is open, 
, 
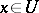is a mapping of class 
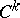, is then called a 
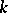-jet from 
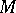to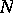 
. Equivalence is defined thus:
 |
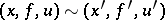if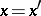 
and if the local images of the mappings 
, 
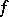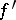at 
in relation to a pair of charts have identical derivatives up to the order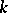 
, inclusive. The space of jets 
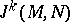is a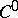 
-manifold.
References
| [1] | P. Bröcker, L. Lander, "Differentiable germs and catastrophes" , Cambridge Univ. Press (1975) |
| [2] | W. Guillemin, "Stable mappings and their singularities" , Springer (1973) |
| [3] | T. Poston, I. Stewart, "Catastrophe theory and its applications" , Pitman (1978) |
How to Cite This Entry:
Jet. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Jet&oldid=17431
Jet. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Jet&oldid=17431
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article