Lebesgue criterion
From Encyclopedia of Mathematics
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
A criterion for pointwise convergence of Fourier series. If a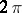 
-periodic function 
, integrable on the interval 
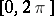, satisfies the condition
 | (*) |
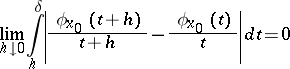at a point 
for some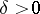 
, where
 |
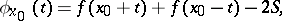then the Fourier series of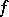 
at 
converges to the number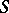 
. The criterion was proved by H. Lebesgue [1]. Condition (*) is equivalent to the aggregate of the two conditions
 |
 |
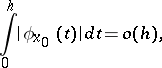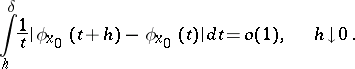The Lebesgue criterion is more powerful then the Dirichlet criterion (convergence of series); the Jordan criterion; the Dini criterion; the de la Vallée-Poussin criterion; and the Young criterion.
References
| [1] | H. Lebesgue, "Récherches sur le convergence des séries de Fourier" Math. Ann. , 61 (1905) pp. 251–280 |
| [2] | N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian) |
Comments
References
| [a1] | A. Zygmund, "Trigonometric series" , 1–2 , Cambridge Univ. Press (1988) |
How to Cite This Entry:
Lebesgue criterion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lebesgue_criterion&oldid=17261
Lebesgue criterion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lebesgue_criterion&oldid=17261
This article was adapted from an original article by B.I. Golubov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article