Suslin condition

A condition that arose when the Suslin hypothesis was stated. A topological space (a Boolean algebra, a partially ordered set) satisfies the Suslin condition if and only if every family of non-empty disjoint open subsets (of non-zero pairwise incompatible elements) is countable. The Suslin condition has been generalized to include an arbitrary cardinal number; the corresponding cardinal-valued invariant is the Suslin number.

Comments

In partially ordered sets, the Suslin condition is commonly called the countable anti-chain condition. In Boolean algebras, it is equivalent to the assertion that every totally ordered subset is countable; for this reason it is often called the countable chain condition, and this usage is also (misleadingly) applied to partially ordered sets.

The Suslin number of a topological space 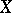is the minimum cardinal number 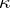such that every pairwise disjoint family of open subsets of 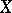has cardinality less than 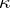. This is closely related to the cellularity: the supremum of the cardinalities of pairwise disjoint families of open subsets.

References

[a1]	W.W. Comfort, S. Negrepontis, "Chain conditions in topology" , Cambridge Univ. Press (1982)