Bifunctor

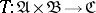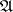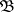A mapping , defined on the Cartesian product of two categories and with values in 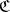, which assigns to each pair of objects 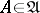, 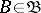some object 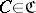, and to each pair of morphisms

the morphism

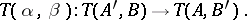(1)

The following conditions

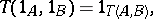(2)

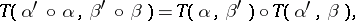must also be met. In such a case one says that the functor 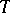is contravariant with respect to the first argument and covariant with respect to the second.

Comments

What is described above is a bifunctor contravariant in its first argument and covariant in its second. A bifunctor covariant in both arguments, the more fundamental notion ([a1]), has (1) and (2) replaced by

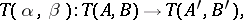(1prm)

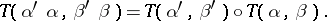(2prm)

Similarly one can define bifunctors contravariant in both arguments and covariant in the first and contravariant in the second argument.

References

[a1]	B. Mitchell, "Theory of categories" , Acad. Press (1965)