Cohn-Vossen transformation
A correspondence between a pair of isometric surfaces  and
and  and an infinitesimal deformation of the so-called mean surface
and an infinitesimal deformation of the so-called mean surface  : If
: If  and
and  are the radius (position) vectors of the surfaces
are the radius (position) vectors of the surfaces  and
and  , then the radius vector
, then the radius vector  of
of  is given by
is given by  , and the field of velocities
, and the field of velocities  of the infinitesimal deformation
of the infinitesimal deformation 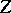 is
is  . It was introduced by S.E. Cohn-Vossen [1]. If
. It was introduced by S.E. Cohn-Vossen [1]. If  and
and  are smooth surfaces and if the angle between the semi-tangents
are smooth surfaces and if the angle between the semi-tangents 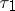 and
and 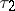 to the curves on
to the curves on  and
and 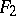 corresponding under the isometry is less than
corresponding under the isometry is less than 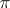 , then
, then 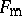 turns out to be smooth. This fact has enabled one to reduce in a number of cases the study of the isometry of
turns out to be smooth. This fact has enabled one to reduce in a number of cases the study of the isometry of 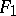 and
and 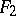 to the study of infinitesimal deformations (cf. Infinitesimal deformation) of
to the study of infinitesimal deformations (cf. Infinitesimal deformation) of 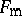 . For fixed points
. For fixed points 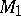 on
on 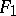 and
and 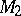 on
on 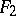 the Cohn-Vossen transformation defines a Cayley transformation of the orthogonal matrix
the Cohn-Vossen transformation defines a Cayley transformation of the orthogonal matrix 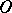 , representing the isometry of the tangent space to
, representing the isometry of the tangent space to 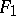 to that of
to that of 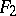 , into a skew-symmetric matrix describing the infinitesimal deformation of
, into a skew-symmetric matrix describing the infinitesimal deformation of  .
.
The Cohn-Vossen transformation can be generalized to the case of spaces of constant curvature [2].
References
| [1] | S.E. Cohn-Vossen, "Some problems of differential geometry in the large" , Moscow (1959) (In Russian) |
| [2] | A.V. Pogorelov, "Extrinsic geometry of convex surfaces" , Amer. Math. Soc. (1972) (Translated from Russian) |
Comments
For this type of infinitesimal deformation one also uses the term infinitesimal bending. The mean surface  is the special case
is the special case  of the mixture of isometric surfaces
of the mixture of isometric surfaces 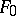 and
and  defined by the points in space dividing the segments joining corresponding points (under the isometry) in the ratio
defined by the points in space dividing the segments joining corresponding points (under the isometry) in the ratio  . The study of these mixtures is an important tool in the isotopy problem of convex surfaces (cf. Convex surface and [2], Chapt. 3, Para. 3).
. The study of these mixtures is an important tool in the isotopy problem of convex surfaces (cf. Convex surface and [2], Chapt. 3, Para. 3).
Cohn-Vossen transformation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cohn-Vossen_transformation&oldid=16863