Keldysh-Lavrent'ev example
An example of a simply-connected domain 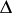 in the complex
in the complex  -plane bounded by a rectifiable Jordan curve but not belonging to the class
-plane bounded by a rectifiable Jordan curve but not belonging to the class 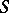 of Smirnov domains (cf. Smirnov domain).
of Smirnov domains (cf. Smirnov domain).
Let 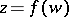 be a function realizing a conformal mapping of the unit disc
be a function realizing a conformal mapping of the unit disc 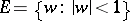 onto a simply-connected domain
onto a simply-connected domain 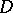 bounded by a rectifiable Jordan curve. It is known that
bounded by a rectifiable Jordan curve. It is known that 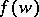 is continuous and one-to-one in the closed disc
is continuous and one-to-one in the closed disc 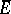 and that the logarithm of the modulus of the derivative
and that the logarithm of the modulus of the derivative 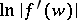 can be represented in
can be represented in 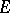 by the Poisson–Stieltjes integral
by the Poisson–Stieltjes integral
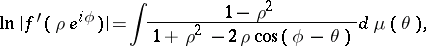 | (*) |
where 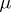 is the normalized Borel measure on
is the normalized Borel measure on 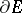 ,
, 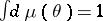 . The class
. The class 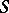 consists of those closed domains
consists of those closed domains 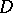 for which the measure
for which the measure 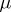 in the representation (*) is absolutely continuous with respect to the Lebesgue measure on
in the representation (*) is absolutely continuous with respect to the Lebesgue measure on 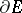 and the integral (*) becomes the Poisson–Lebesgue integral (cf. Poisson integral) of the boundary values
and the integral (*) becomes the Poisson–Lebesgue integral (cf. Poisson integral) of the boundary values  , which exist almost-everywhere on
, which exist almost-everywhere on  .
.
M.V. Keldysh and M.A. Lavrent'ev [1] constructed for any 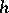 ,
, 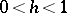 , a simply-connected domain
, a simply-connected domain 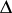 bounded by a rectifiable Jordan curve
bounded by a rectifiable Jordan curve 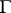 , located in the disc
, located in the disc 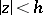 ,
, 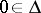 , such that under a conformal mapping of
, such that under a conformal mapping of 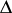 onto
onto 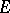 ,
,
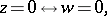 |
and the image of any arc 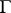 on the circle
on the circle 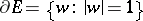 is an arc of the same length. This domain
is an arc of the same length. This domain 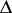 does not belong to the class
does not belong to the class 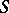 , since
, since 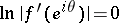 almost-everywhere on
almost-everywhere on 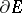 .
.
A complete solution of the problem of characterizing domains of class 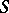 (domains of Smirnov type) has so far (1989) not been obtained (see [2], [3]).
(domains of Smirnov type) has so far (1989) not been obtained (see [2], [3]).
References
| [1] | M.V. Keldysh, M.A. Lavrent'ev, "Sur la répresentation conforme des domains limités par des courbes rectifiables" Ann. Ecole Norm. Sup. , 54 (1937) pp. 1–38 |
| [2] | I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
| [3] | A.J. Lohwater, "The boundary behaviour of analytic functions" Itogi Nauk. i Tekhn. Mat. Anal. , 10 (1973) pp. 99–259 (In Russian) |
Comments
The construction of Keldysh and Lavrent'ev is extraordinarily complicated. For a more accessible treatment, see [a1] and [a2].
References
| [a1] | P.L. Duren, H.S. Shapiro, A.L. Shields, "Singular measures and domains not of Smirnov type" Duke Math. J. , 33 (1966) pp. 247–254 |
| [a2] | G. Piranian, "Two monotonic, singular, uniformly almost smooth functions" Duke Math. J. , 33 (1966) pp. 254–262 |
Keldysh-Lavrent'ev example. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Keldysh-Lavrent%27ev_example&oldid=16860