Minimal polynomial of a matrix
From Encyclopedia of Mathematics
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
minimum polynomial of a matrix
Let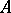 
be a matrix. The minimal polynomial of 
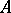is the monic polynomial 
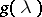of lowest degree such that 
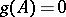. It divides the characteristic polynomial of 
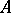and, more generally, it divides every polynomial 
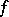such that 
.
References
| [a1] | L. Mirsky, "An introduction to linear algebra" , Dover, reprint (1990) pp. 203ff |
| [a2] | Ch.G. Cullen, "Matrices and linear transformations" , Dover, reprint (1990) pp. 178ff |
How to Cite This Entry:
Minimal polynomial of a matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Minimal_polynomial_of_a_matrix&oldid=16850
Minimal polynomial of a matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Minimal_polynomial_of_a_matrix&oldid=16850
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article