Separable semi-group
From Encyclopedia of Mathematics
A semi-group in which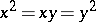 
for elements 
, 
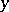implies that 
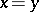. If a semi-group 
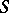has a partition into sub-semi-groups that satisfy the cancellation law, then 
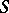is separable. For commutative semi-groups the converse holds; moreover, any commutative separable semi-group can be expanded into a band of semi-groups (trivially into a semi-lattice) with the cancellation law. A commutative semi-group is separable if and only if it can be imbedded in a Clifford semi-group. A periodic semi-group is separable if and only if it is a Clifford semi-group. A commutative semi-group 
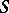is separable if and only if its characters separate the elements of 
.
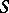References
| [1] | A.H. Clifford, G.B. Preston, "The algebraic theory of semigroups" , 1 , Amer. Math. Soc. (1961) |
How to Cite This Entry:
Separable semi-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Separable_semi-group&oldid=16817
Separable semi-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Separable_semi-group&oldid=16817
This article was adapted from an original article by L.N. Shevrin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article