Contextual grammar
A language-generating device based on the operation of adjoining contexts to strings, according to a selection procedure. Such grammars were introduced (in the external variant, with the contexts adjoined at the ends of the currently generated string) in [a2], with the explicit purpose of obtaining an intrinsic generative mechanism, without auxiliary symbols (as in Chomsky grammars) and making use of the string-context interplay which is fundamental in all linguistic theories. For modelling natural language-syntactical constructions, the internal contextual grammars, introduced in [a5], turned out to be more useful.
Let 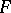 be a family of languages. An internal contextual grammar with
be a family of languages. An internal contextual grammar with  -selection is a system
-selection is a system
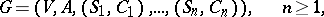 |
where 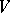 is an alphabet,
is an alphabet, 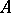 is a finite language over
is a finite language over 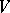 ,
, 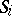 are languages (over
are languages (over  ) in the family
) in the family 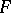 , and
, and 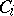 are finite sets of contexts over
are finite sets of contexts over  , i.e., pairs
, i.e., pairs 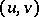 ,
, 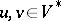 ,
, 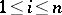 . The elements of
. The elements of 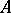 are axioms,
are axioms, 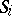 are the selectors of the productions
are the selectors of the productions 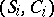 ,
, 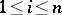 . With respect to
. With respect to 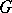 , for
, for 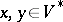 one writes
one writes 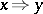 if and only if
if and only if 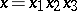 ,
, 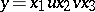 , with
, with 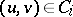 ,
, 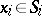 , for certain
, for certain 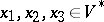 ,
, 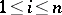 . (The contexts in
. (The contexts in 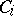 can be adjoined to strings in the associated selector
can be adjoined to strings in the associated selector 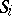 .)
.)
Denoting by 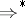 the reflexive and transitive closure of
the reflexive and transitive closure of 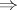 , the language generated by
, the language generated by 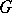 can be defined by
can be defined by
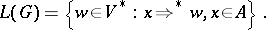 |
Let 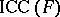 be the family of languages generated by internal contextual grammars with
be the family of languages generated by internal contextual grammars with 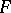 -selection. Denote by
-selection. Denote by 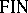 ,
, 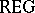 ,
, 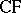 ,
, 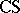 ,
, 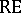 ,
, 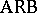 the families of finite, regular, context-free, context-sensitive, recursively enumerable, and arbitrary languages, respectively. Some basic results for contextual grammars are as follows:
the families of finite, regular, context-free, context-sensitive, recursively enumerable, and arbitrary languages, respectively. Some basic results for contextual grammars are as follows:
1) 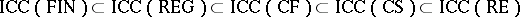 ;
;
2) 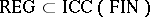 ,
, 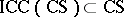 ;
;
3) 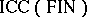 contains non-semi-linear languages;
contains non-semi-linear languages;
4) all families 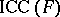 ,
, 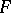 as above, are anti-AFL (cf. Trio; Abstract family of languages);
as above, are anti-AFL (cf. Trio; Abstract family of languages);
5) every recursively enumerable language  can be written in the form
can be written in the form 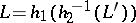 , where
, where 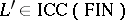 ,
, 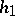 is a weak coding and
is a weak coding and 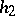 is a morphism.
is a morphism.
A lot of variants have been considered (left-most, prefix, parallel, blocked derivation, maximal or minimal use of selectors, one-sided contexts, deterministic grammars, etc.). Details can be found in [a1], [a3], [a4].
References
| [a1] | A. Ehrenfeucht, Gh. Păun, G. Rozenberg, "Contextual grammars" G. Rozenberg (ed.) A. Salomaa (ed.) , Handbook of Formal Languages , Springer (1996) |
| [a2] | S. Marcus, "Contextual grammars" Rev. Roum. Math. Pures Appl. , 14 (1969) pp. 1525–1534 |
| [a3] | Gh. Păun, "Contextual grammars" , Publ. House of the Romanian Acad., Bucharest (1982) (In Rumanian) |
| [a4] | Gh. Păun, "Marcus contextual grammars. After 25 years" Bull. EATCS , 52 (1994) pp. 263–273 |
| [a5] | Gh. Păun, X.M. Nguyen, "On the inner contextual grammars" Rev. Roum. Math. Pures Appl. , 25 (1980) pp. 641–651 |
Contextual grammar. Gh. Păun (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Contextual_grammar&oldid=16521