Pseudo-Galilean space

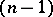A projective -space (cf. Projective space) with a distinguished infinitely-distant -plane 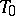in the affine -space (cf. Affine space) in which in turn an infinitely-distant 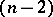-plane 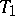of the pseudo-Euclidean space 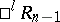has been distinguished, while i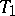n an 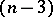-quadric 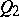has been distinguished which is the absolute of the hyperbolic 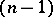-space of index 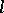. The family of planes 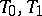and quadric 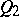forms the absolute (basis) of the pseudo-Galilean space; the latter is denoted by 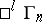. E.g., -space 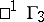has as absolute a -plane 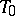, a straight line 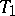in 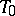and a pair of real points 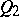on 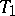. A pseudo-Galilean space can be defined as an affine -space in whose infinitely-distant hyperbolic hyperplane under completion to projective -space the geometry of the pseudo-Euclidean 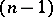-space of index 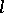has been defined.

The distance between points is defined analogously to the distance in a Galilean space.

The motions of 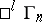are its collineations mapping the absolute into itself. The motions form a group, which is a Lie group.

The space whose absolute is dual to the absolute of 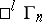is called a co-pseudo-Galilean space. A flag space is a limit case of .

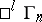References

[1]	B.A. Rozenfel'd, "Non-Euclidean spaces" , Moscow (1969) (In Russian)

References

[a1]	H.S.M. Coxeter, "Non-Euclidean geometry" , Univ. Toronto Press (1968)
[a2]	S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978) pp. Chapt. X