Beurling algebra

of Fourier series with summable majorant of coefficients

An algebra closely related to the Wiener algebra

where

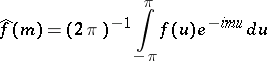is the 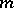th Fourier coefficient of 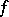(cf. also Fourier coefficients). The Beurling algebra is defined as

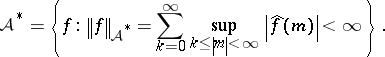The space 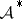was introduced by A. Beurling for establishing contraction properties of functions [a2]: Let

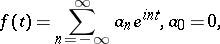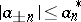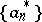be an absolutely convergent Fourier series such that , , where is a non-increasing sequence of numbers with a finite sum. Then if

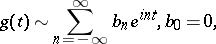is a contraction of 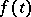(that is, for any pair of arguments 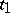, 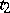the inequality 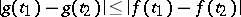holds), then the Fourier series of 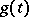also converges absolutely, and

A similar result was proved in [a2] for the Fourier transform, whence integrability of the monotone majorant on the real line is considered. These two spaces coincide locally, hence have much in common.

Subsequently, 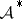appeared in some other papers either in explicit or implicit form. See [a1] for a detailed survey of the history and properties of .

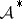It turned out that the consideration of summability of Fourier series by linear methods at Lebesgue points leads to the same space of functions. Let 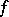be a 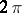-periodic integrable function with Fourier series 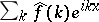. Let 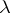be a continuous function on 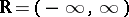, representable as follows:

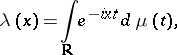where 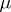is a finite Borel measure satisfying 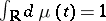. Consider the means

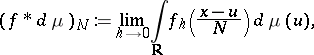where

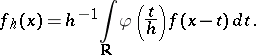Here, 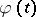is infinitely differentiable, equal to 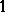for 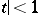, vanishing for 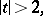and such that 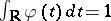. For 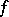sufficiently smooth one has

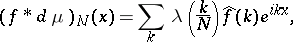and these are the linear means of the Fourier series generated by .

The linear means 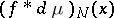converge to 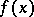as 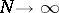at all the Lebesgue points of each integrable 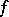if and only if the measure is absolutely continuous (cf. Absolute continuity) with respect to the Lebesgue measure and

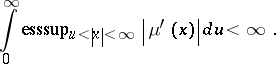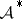possesses many properties which are similar to those of :

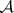1) is a Banach algebra with the local property.

2) The space of maximal ideals (cf. also Maximal ideal) of 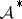coincides with .

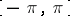3) 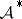is a regular Banach algebra with trivial radical.

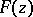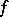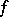4) If and is defined and analytic on a neighbourhood of the set of values of the function , then (in particular, if does not vanish anywhere, then ).

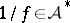The space 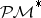of all sequences 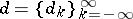with finite norm

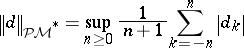is the dual space of .

The space 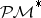is not separable (cf. also Separable space) and thus the space 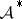, like 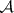, is not reflexive (cf. also Reflexive space).

Spectral properties of .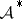

The following two results are analogues for 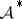of the Herz theorem and of the Wiener–Ditkin theorem, respectively.

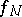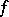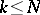Let be a function coinciding with at each point , where are integers, , and 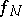is linear on intervals. Suppose 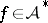. Then

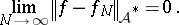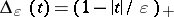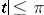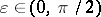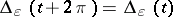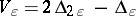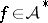Let for and , , and . Let and 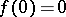. Then

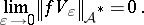Synthesis problems.

Writing 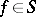if admits synthesis in the norm of 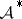(cf. also Synthesis problems), for the following statements hold.

a) If 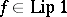, then 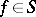( 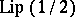for ).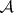

b) If 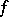is absolutely continuous and in 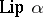, , 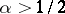then 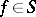(for , 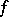has to be of bounded variation).

(Here, analogous conditions for 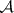are given in parentheses; these assertions make up the Beurling–Pollard theorem.)

The following statements describe structural properties of functions in . In the sequel, 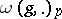stands for the modulus of continuity, in the norm of 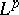, of a function 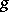(cf. also Continuity, modulus of).

i) 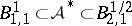, and the imbeddings into these Besov spaces (cf. also Nikol'skii space and Hankel operator) are both continuous.

ii) If 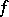is absolutely continuous and

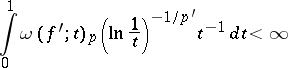for some 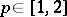, , 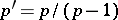then .

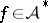iii) There exists a continuously differentiable function 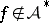for which

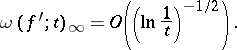The second inclusion in i) is sharp; indeed, for each 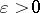there exists a function 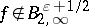such that 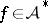. As for ii), it is sharp for 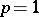. The question is open for 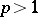(as of 2000).

There exists a function 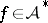that is not of bounded variation (cf. also Function of bounded variation).

The following condition, although being very simple, is surprisingly sharp. If 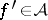, then 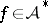. If the Fourier series of 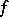is lacunary in the sense of Hadamard (cf. also Lacunary sequence), then the converse statement holds.

Note that the central problem of spectral synthesis, that is, existence of sets that are not of synthesis as well as existence of functions not admitting synthesis, is still open (as of 2000) for .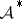

Another open question is connected with Beurling's initial result. It would be interesting to know whether the following statement, converse to that given above, is true or not: If for every 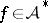one has 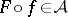, then .

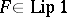Some of the results known for 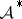have been generalized to the multi-dimensional case.

References

[a1]	E. Belinsky, E. Liflyand, R. Trigub, "The Banach algebra and its properties" J. Fourier Anal. Appl. , 3 (1997) pp. 103–129
[a2]	A. Beurling, "On the spectral synthesis of bounded functions" Acta Math. , 81 (1949) pp. 225–238
[a3]	J.-P. Kahane, "Séries de Fourier absolument convergentes" , Springer (1970)