Graph homeomorphism
From Encyclopedia of Mathematics
An equivalence relation on the set of graphs, characterizing their geometric properties. The notion of a graph homeomorphism is defined as follows. Subdivision of an edge 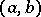 of a graph
of a graph 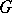 is an operation involving the addition of a new vertex
is an operation involving the addition of a new vertex  , the removal of
, the removal of  , and the addition of two new edges
, and the addition of two new edges 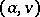 and
and 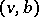 . Geometrically, this operation consists in addition of some (interior) point
. Geometrically, this operation consists in addition of some (interior) point  on the line
on the line 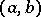 ; this point then becomes a new vertex. A graph
; this point then becomes a new vertex. A graph 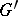 is called a subdivision of a graph
is called a subdivision of a graph 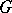 if it can be obtained from
if it can be obtained from 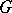 by repeating the operation of edge subdivision several times. Two graphs
by repeating the operation of edge subdivision several times. Two graphs 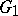 and
and  are said to be homeomorphic if they have isomorphic subdivisions (cf. Graph isomorphism).
are said to be homeomorphic if they have isomorphic subdivisions (cf. Graph isomorphism).
How to Cite This Entry:
Graph homeomorphism. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Graph_homeomorphism&oldid=16244
Graph homeomorphism. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Graph_homeomorphism&oldid=16244
This article was adapted from an original article by V.B. Alekseev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article