Infra-barrelled space

A locally convex linear topological space in which every barrel (i.e. absorbing convex closed balanced set) absorbing any bounded set is a neighbourhood of zero. The barrelled spaces form an important class of infra-barrelled spaces (cf. Barrelled space).

Inductive limits and arbitrary products of infra-barrelled spaces are infra-barrelled. A space is infra-barrelled if and only if either every bounded lower semi-continuous semi-norm is continuous, or if every strongly-bounded subset in the dual space (cf. Adjoint space) is equicontinuous (cf. Equicontinuity). In particular, every bornological space (i.e. a space in which every bounded semi-norm is continuous) is an infra-barrelled space. 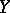In a sequentially-complete linear topological space infra-barrelledness implies barrelledness; infra-barrelled spaces, like barrelled spaces, can be characterized in terms of mappings into Banach spaces: A locally convex linear topological space is infra-barrelled if and only if for any Banach space every linear mapping from into 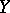with a closed graph and that maps bounded sets into bounded sets is continuous. See also Ultra-barrelled space.

References

[1]	N. Bourbaki, "Elements of mathematics. Topological vector spaces" , Addison-Wesley (1977) (Translated from French)
[2]	R.E. Edwards, "Functional analysis: theory and applications" , Holt, Rinehart & Winston (1965)

Comments

"Infra-barrelled spaces" are also called quasi-barrelled spaces.

References

[a1]	H. Janchow, "Locally convex spaces" , Teubner (1981)