Pseudo-quadratic form
From Encyclopedia of Mathematics
Let 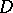 be a division ring (cf. Division algebra) with centre
be a division ring (cf. Division algebra) with centre 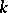 and let
and let 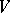 be a right vector space over
be a right vector space over 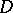 . Let
. Let 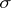 be an automorphism of
be an automorphism of 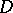 and
and 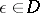 such that
such that 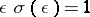 ,
, 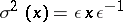 for all
for all 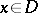 . Assume also that
. Assume also that 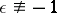 if
if 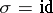 and
and 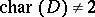 . Set
. Set
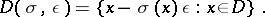 |
This is an additive subgroup of 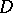 . Let
. Let 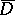 be the quotient
be the quotient 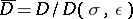 , and let
, and let 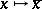 denote the quotient mapping
denote the quotient mapping 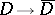 . A pseudo-quadratic form on
. A pseudo-quadratic form on 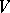 is a function
is a function  such that there exists a trace-valued
such that there exists a trace-valued 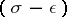 -Hermitian form (cf. Sesquilinear form)
-Hermitian form (cf. Sesquilinear form) 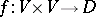 such that
such that 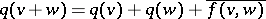 . The form
. The form  is uniquely determined by this and is called the sesquilinearization of
is uniquely determined by this and is called the sesquilinearization of 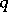 .
.
A  -pseudo-quadratic form is a quadratic form in the usual sense. The Witt index of a pseudo-quadratic form is that of the associated sesquilinear form.
-pseudo-quadratic form is a quadratic form in the usual sense. The Witt index of a pseudo-quadratic form is that of the associated sesquilinear form.
References
| [a1] | J. Tits, "Buildings and BN-pairs of spherical type" , Springer (1974) pp. Sect. 8.2 |
| [a2] | N. Bourbaki, "Eléments de mathématique. Algèbre" , Hermann (1959) pp. Chapt. 9. Formes sesquilinéaires et formes quadratiques |
| [a3] | J.A. Dieudonné, "La géométrie des groups classiques" , Springer (1963) |
How to Cite This Entry:
Pseudo-quadratic form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pseudo-quadratic_form&oldid=15903
Pseudo-quadratic form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pseudo-quadratic_form&oldid=15903