Frobenius conjecture
In 1903, G. Frobenius published in [a1] his least known result on finite groups. He proved that if  is a divisor of the order of a finite group
is a divisor of the order of a finite group  , then the number of solutions of
, then the number of solutions of  in
in 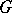 is a multiple of
is a multiple of  . This result was greatly generalized by Ph. Hall in [a3]. In his book [a2], M. Hall proved the following generalization of Frobenius' theorem: If
. This result was greatly generalized by Ph. Hall in [a3]. In his book [a2], M. Hall proved the following generalization of Frobenius' theorem: If  is a finite group of order
is a finite group of order  and
and  is a conjugacy class of
is a conjugacy class of  of cardinality
of cardinality 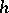 , then the number of solutions of
, then the number of solutions of 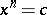 in
in  , when
, when  ranges over
ranges over 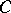 , is a multiple of the greatest common divisor
, is a multiple of the greatest common divisor  .
.
The Frobenius conjecture deals with a special case of the result proved by Frobenius. It claims that if  is a divisor of the order of the finite group
is a divisor of the order of the finite group 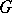 and if the number of solutions of
and if the number of solutions of 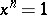 in
in 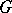 is exactly
is exactly  , then these solutions form a normal subgroup of
, then these solutions form a normal subgroup of  . It is clear that one needs only to prove the closure of the set of solutions. Thus, the conjecture holds in Abelian groups (cf. also Abelian group). It is also easy to see that it suffices to show that
. It is clear that one needs only to prove the closure of the set of solutions. Thus, the conjecture holds in Abelian groups (cf. also Abelian group). It is also easy to see that it suffices to show that 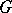 contains a subgroup of order
contains a subgroup of order  . Hence, the conjecture certainly holds whenever
. Hence, the conjecture certainly holds whenever 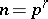 , a power of a prime number, since
, a power of a prime number, since  contains a subgroup of order
contains a subgroup of order  by one of the Sylow theorems. In [a2], M. Hall proved the conjecture for solvable groups (cf. also Solvable group). Still, the general problem remained open for a long period and it was solved only recently (1998), using the classification of the finite simple groups (cf. also Simple finite group). It is worthwhile to mention that the assumption that
by one of the Sylow theorems. In [a2], M. Hall proved the conjecture for solvable groups (cf. also Solvable group). Still, the general problem remained open for a long period and it was solved only recently (1998), using the classification of the finite simple groups (cf. also Simple finite group). It is worthwhile to mention that the assumption that  is a divisor of the order of
is a divisor of the order of  is essential. Thus, for example,
is essential. Thus, for example,  has exactly
has exactly 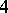 solutions in the symmetric group on three letters, but obviously the solutions do not form a subgroup of
solutions in the symmetric group on three letters, but obviously the solutions do not form a subgroup of  .
.
Connection with the classification problem.
It was shown in 1954 by R.A. Zemlin in his PhD thesis [a6] that it suffices to prove the conjecture for non-Abelian simple groups. In other words, one needs to prove that if 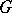 is a simple group and
is a simple group and  is a divisor of
is a divisor of  , then the number of solutions of
, then the number of solutions of 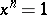 equals
equals  only for the trivial values of
only for the trivial values of  :
:  or
or  . In [a5] M. Murai proved the same result and showed, in addition, that it suffices to consider those divisors
. In [a5] M. Murai proved the same result and showed, in addition, that it suffices to consider those divisors  of
of  which satisfy
which satisfy  .
.
The conjecture has been verified for the alternating groups, the sporadic groups and the finite simple groups of Lie type by M.J. Rust, H. Yamaki and N. Iiyori in a long series of papers, the last and concluding one being [a4].
References
| [a1] | G. Frobenius, "Über einen Fundamentalsatz der Gruppentheorie" Berl. Sitz. (1903) pp. 987–991 |
| [a2] | M. Hall, "The theory of groups" , Macmillan (1959) |
| [a3] | P. Hall, "On a theorem of Frobenius" Proc. London Math. Soc. , 7 : 3 (1956) pp. 1–42 |
| [a4] | N. Iiyori, "A conjecture of Frobenius and the simple groups of Lie type, IV" J. Algebra , 154 (1993) pp. 188–214 |
| [a5] | M. Murai, "On the Frobenius conjecture" SÛgaku , 35 (1983) pp. 82–84 (In Japanese) |
| [a6] | R.A. Zemlin, "On a conjecture arising from a theorem of Frobenius" PhD Thesis Ohio State Univ. (1954) |
Frobenius conjecture. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Frobenius_conjecture&oldid=15708