Spinodal decomposition
A term introduced in the physical description of unmixing of metallic alloys by J.W. Cahn [a1], cf. Fig.a1.
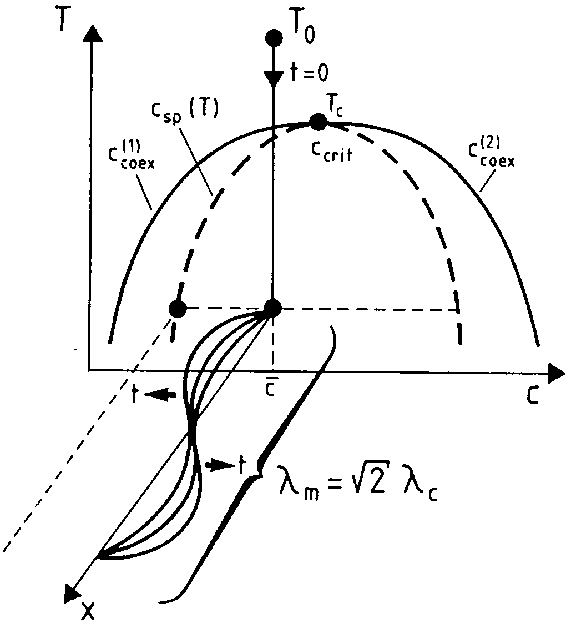
Figure: s110240a
Schematic plot of a "quenching experiment" of a mixture and the resulting build-up of concentration fluctuations in a mixture. Shown is the temperature (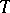 ) versus concentration (
) versus concentration ( ) plane, while the third axis (
) plane, while the third axis ( ) is a spacial coordinate.
) is a spacial coordinate.
The thermodynamic state of such a mixture is described by the variables temperature 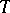 and relative concentration
and relative concentration  , and one considers a situation where in the "phase diagram" of this system one finds a "miscibility gap" , i.e. there is a curve in the
, and one considers a situation where in the "phase diagram" of this system one finds a "miscibility gap" , i.e. there is a curve in the 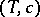 -plane in Fig.a1 (this curve is labelled by the two branches
-plane in Fig.a1 (this curve is labelled by the two branches 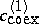 ,
, 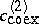 in Fig.a1, which merge in a critical point
in Fig.a1, which merge in a critical point 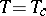 ,
, 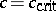 ) underneath which the system cannot exist in a state of homogeneous concentration
) underneath which the system cannot exist in a state of homogeneous concentration  in thermal equilibrium, while it does exist in such a state above this curve (e.g., in the initial state at a temperature
in thermal equilibrium, while it does exist in such a state above this curve (e.g., in the initial state at a temperature 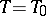 ,
, 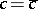 in Fig.a1).
in Fig.a1).
One now considers a rapid cooling experiment (quenching) where the system is brought at time 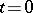 from this temperature
from this temperature 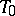 above the coexistence curve to a temperature
above the coexistence curve to a temperature 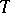 below the so-called spinodal curve
below the so-called spinodal curve 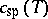 , defined by the condition that the second derivative
, defined by the condition that the second derivative 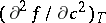 of the free energy density
of the free energy density 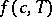 vanishes. In this regime, the homogeneous state is intrinsically unstable, as is found from a linear stability analysis of concentration fluctuations [a1]. According to such a linear stability analysis, all long wavelength concentration fluctuations with wavelengths exceeding a critical wavelength
vanishes. In this regime, the homogeneous state is intrinsically unstable, as is found from a linear stability analysis of concentration fluctuations [a1]. According to such a linear stability analysis, all long wavelength concentration fluctuations with wavelengths exceeding a critical wavelength 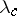 are unstable, and the maximum growth rate occurs at a wavelength
are unstable, and the maximum growth rate occurs at a wavelength 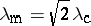 . While, according to such a linear theory, one would expect that this wavelength dominates in the late stages of the phase separation process (Fig.a1), actually the process is highly non-linear [a2], and so-called "coarsening" occurs (there is a dominant wavelength
. While, according to such a linear theory, one would expect that this wavelength dominates in the late stages of the phase separation process (Fig.a1), actually the process is highly non-linear [a2], and so-called "coarsening" occurs (there is a dominant wavelength 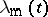 , but it depends upon the time
, but it depends upon the time 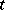 after the start of the process,
after the start of the process,  as
as 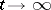 [a2]).
[a2]).
If the thermal fluctuations are neglected, spinodal decomposition is described by the following non-linear diffusion equation for the local concentration 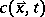 at a point
at a point 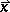 of
of 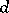 -dimensional infinitely extended space:
-dimensional infinitely extended space:
 | (a1) |
where 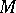 has the physical meaning of a mobility,
has the physical meaning of a mobility, 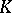 comes from a gradient energy contribution,
comes from a gradient energy contribution, 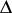 denotes the Laplace operator, and the free energy density
denotes the Laplace operator, and the free energy density 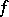 can, e.g., be written in terms of
can, e.g., be written in terms of 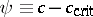 as
as
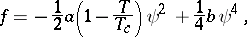 |
with  ,
, 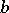 constants. A parabolic spinodal curve results from
constants. A parabolic spinodal curve results from
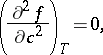 |
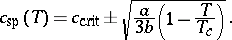 |
The linear stability analysis of (a1) yields, writing 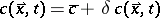 ,
,
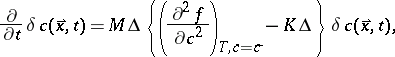 | (a2) |
and is solved by introducing spacial Fourier transforms,  , i.e., one finds an exponential time dependence (
, i.e., one finds an exponential time dependence (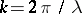 ),
),
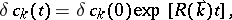 | (a3) |
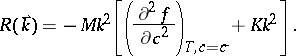 |
One sees from (a3) that the rate 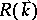 is positive if
is positive if
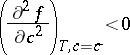 |
and
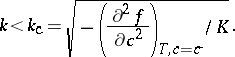 |
The "critical wavelength" mentioned above is 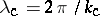 .
.
Of course, it is clear that the linear analysis is relevant at best for the early stages of the process. Solving the full non-linear partial differential equations (a1) is a challenging problem of numerical mathematics. For applications in physics additional complications occur: in the initial stages of unmixing, the deterministic equation (a1) needs to be amended by a stochastic "random force" term to represent statistical fluctuations. In addition there occurs a coupling to further dynamical variables (in solids: the elastic displacement field 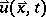 ; in fluid mixtures: the velocity field
; in fluid mixtures: the velocity field 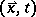 ). Nevertheless, (a1) is a very useful starting point, and numerous experimental applications exist [a2].
). Nevertheless, (a1) is a very useful starting point, and numerous experimental applications exist [a2].
References
| [a1] | J.W. Cahn, "On spinodal decomposition" Acta Metall. , 9 (1961) pp. 795–801 |
| [a2] | K. Binder, "Spinodal decomposition" P. Haasen (ed.) , Materials Science and Technology. Phase Transformations in Materials , 5 , VCH (1991) pp. 405–471 |
Spinodal decomposition. K. Binder (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Spinodal_decomposition&oldid=15567