P-point
As defined in [a1], a point in a completely-regular space 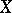 at which any prime ideal of the ring
at which any prime ideal of the ring  of real-valued continuous functions is maximal (cf. also Continuous function; Maximal ideal). A prime ideal
of real-valued continuous functions is maximal (cf. also Continuous function; Maximal ideal). A prime ideal 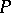 is "at x" if
is "at x" if 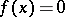 for all
for all 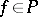 ; thus
; thus  is a
is a 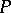 -point if and only if
-point if and only if 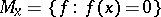 is the only prime ideal at
is the only prime ideal at  . Equivalent formulations are:
. Equivalent formulations are:
1) if 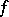 is a continuous function and
is a continuous function and 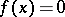 , then
, then 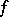 vanishes on a neighbourhood of
vanishes on a neighbourhood of  ; and
; and
2) every countable intersection of neighbourhoods of  contains a neighbourhood of
contains a neighbourhood of  . The latter is commonly used to define
. The latter is commonly used to define 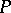 -points in arbitrary topological spaces.
-points in arbitrary topological spaces.
Of particular interest are 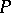 -points in the space
-points in the space 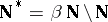 , the remainder in the Stone–Čech compactification of the space of natural numbers. This is so because W. Rudin [a2] proved that the space
, the remainder in the Stone–Čech compactification of the space of natural numbers. This is so because W. Rudin [a2] proved that the space 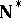 has
has 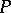 -points if the continuum hypothesis is assumed; this showed that
-points if the continuum hypothesis is assumed; this showed that 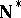 cannot be proved homogeneous (cf. also Homogeneous space), because not every point in an infinite compact space can be a
cannot be proved homogeneous (cf. also Homogeneous space), because not every point in an infinite compact space can be a 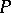 -point. Points of
-point. Points of 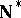 are identified with free ultrafilters on the set
are identified with free ultrafilters on the set 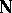 (cf. also Ultrafilter). A point or ultrafilter
(cf. also Ultrafilter). A point or ultrafilter  is a
is a 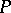 -point if and only if for every sequence
-point if and only if for every sequence 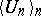 of elements of
of elements of  there is an element
there is an element 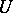 of
of  such that
such that 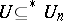 for all
for all  , where
, where 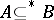 means that
means that 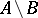 is finite. Equivalently,
is finite. Equivalently,  is a
is a 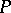 -point if and only if for every partition
-point if and only if for every partition 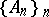 of
of  either there is an
either there is an  such that
such that 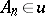 or there is a
or there is a 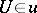 such that
such that 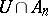 is finite for all
is finite for all  . S. Shelah [a3] constructed a model of set theory in which
. S. Shelah [a3] constructed a model of set theory in which 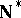 has no
has no 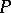 -points, thus showing that Rudin's theorem is not definitive.
-points, thus showing that Rudin's theorem is not definitive.
There is continued interest in 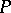 -point ultrafilters because of their combinatorial properties; e.g.,
-point ultrafilters because of their combinatorial properties; e.g.,  is a
is a 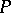 -point if and only if for every function
-point if and only if for every function 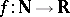 there is an element
there is an element 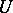 of
of  such that
such that 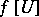 is a converging sequence (possibly to
is a converging sequence (possibly to 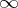 or
or 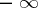 ).
).
References
| [a1] | L. Gillman, M. Henriksen, "Concerning rings of continuous functions" Trans. Amer. Math. Soc. , 77 (1954) pp. 340–362 |
| [a2] | W. Rudin, "Homogeneity problems in the theory of Čech compactifications" Duke Math. J. , 23 (1956) pp. 409–419; 633 |
| [a3] | E. Wimmers, "The Shelah 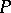 -point independence theorem" Israel J. Math. , 43 (1982) pp. 28–48 -point independence theorem" Israel J. Math. , 43 (1982) pp. 28–48 |
P-point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=P-point&oldid=15552