Infinitely-small function
A function of a variable  whose absolute value becomes and remains smaller than any given number as a result of variation of
whose absolute value becomes and remains smaller than any given number as a result of variation of  . More exactly, a function
. More exactly, a function  defined in a neighbourhood of a point
defined in a neighbourhood of a point 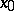 is called an infinitely-small function as
is called an infinitely-small function as  tends to
tends to 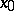 if for any number
if for any number 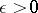 it is possible to find a number
it is possible to find a number 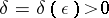 such that
such that 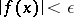 is true for all
is true for all  satisfying the condition
satisfying the condition 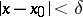 . This fact can be written as follows:
. This fact can be written as follows:
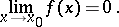 |
Further, the symbolic notation
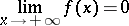 |
means that for any 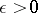 it is possible to find an
it is possible to find an  such that for all
such that for all 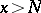 the inequality
the inequality 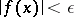 is true. The concept of an infinitely-small function may serve as a base of the general definition of the limit of a function. In fact, the limit of the function
is true. The concept of an infinitely-small function may serve as a base of the general definition of the limit of a function. In fact, the limit of the function 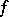 as
as 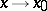 is finite and equal to
is finite and equal to 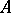 if and only if
if and only if
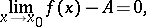 |
i.e. if the function 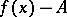 is infinitely small. See also Infinitesimal calculus.
is infinitely small. See also Infinitesimal calculus.
Infinitely-small function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Infinitely-small_function&oldid=15375