Brafman polynomials
From Encyclopedia of Mathematics
Polynomials given by
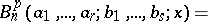 |
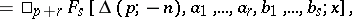 |
where 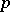 is a positive integer,
is a positive integer, 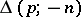 abbreviates the set of
abbreviates the set of 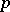 parameters
parameters
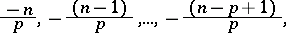 |
and for non-negative integers  and
and  ,
,  denotes the generalized hypergeometric function (cf. also Hypergeometric function), defined by
denotes the generalized hypergeometric function (cf. also Hypergeometric function), defined by
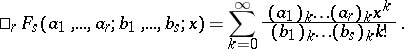 |
The Brafman polynomials arise in the study of generating functions of orthogonal polynomials, [a1].
There are extensions. H.W. Gould and A.T. Hopper [a2] have considered special cases which sometimes reduce to the Hermite polynomials; see [a4] for a generalization. It is known [a3] that, in general, the Brafman polynomials cannot form an orthogonal set with respect to any weight function.
References
| [a1] | F. Brafman, "Some generating functions for Laguerre and Hermite polynomials" Canadian J. Math. , 9 (1957) pp. 180–187 |
| [a2] | H.W. Gould, A.T. Hopper, "Operational formulas connected with two generalizations of Hermite polynomials" Duke Math. J. , 29 (1962) pp. 51–63 |
| [a3] | D. Mangeron, A.M. Krall, D.L. Fernandez, "Weight functions for some new classes of orthogonal polynomials" R. Acad. Cien. (Madrid) , 77 (1983) pp. 597–607 |
| [a4] | R.M. Shreshtha, "On generalized Brafman polynomials" Comp. R. Acad. Bulgar. Sci. , 32 (1979) pp. 1183–1185 |
How to Cite This Entry:
Brafman polynomials. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Brafman_polynomials&oldid=15276
Brafman polynomials. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Brafman_polynomials&oldid=15276
This article was adapted from an original article by A.M. Krall (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article