Pointwise convergence, topology of

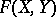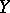One of the topologies on the space of mappings from a set into a topological space . A generalized sequence 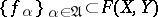converges pointwise to an 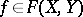if 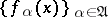converges for any 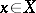to 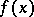in the topology of . The base of neighbourhoods of a point 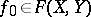is formed by sets of the type 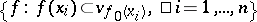, where is a finite set of points in 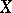and 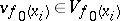is a base of neighbourhoods at the point 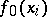in .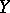

If 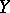is a Hausdorff space, then 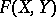is also Hausdorff and 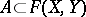is compact if and only if it is closed and for every 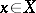the set 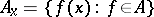is compact.

References

[1]	J.L. Kelley, "General topology" , Springer (1975)

Comments

There has been a lot of research into the interplay between the topological properties of Tikhonov (i.e., completely regular) spaces 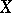and the topological (or linear topological) properties of 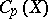, where 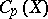is the space of continuous real-valued functions on 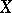, endowed with the topology of pointwise convergence. See [a1].

References

[a1]	A.V. Arkhangel'skii, "A survey of 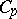-theory" Questions & Answers in Gen. Topol. , 5 (1987) pp. 1–109
[a2]	R. Engelking, "General topology" , Heldermann (1989)