Harmonic majorant

least harmonic majorant of a family

The lower envelope of the family of all superharmonic majorants of the family of subharmonic functions on an open set of a Euclidean space , , i.e.

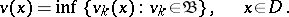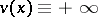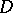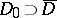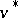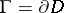The least harmonic majorant is either a harmonic function or on . If the family consists of a single function which is subharmonic on a larger set , the concept of the best harmonic majorant — the solution of the generalized Dirichlet problem for with value on the boundary — may be employed. Always 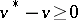, and the following formula [1] is valid:

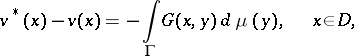where 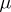is the measure which is associated with , , 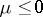and 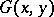is the (generalized) Green function of the Dirichlet problem for 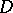. The best and the least harmonic majorants coincide if and only if the set of all irregular points (cf. Irregular boundary point) of 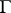has -measure zero.

Correspondingly, if is a family of superharmonic functions on 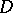, the greatest harmonic minorant of the family 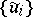is defined as the upper envelope of the family of all subharmonic minorants of 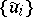; here 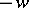is the least harmonic majorant for .

The problem of harmonic majorants may also be posed in terms of the Cauchy problem for the Laplace equation. See Harmonic function.

References

[1]	O. Frostman, "Potentiel d'equilibre et capacité des ensembles avec quelques applications à la théorie des fonctions" Mett. Lunds Univ. Mat. Sem. , 3 (1935) pp. 1–118
[2]	M. Brélot, "Eléments de la théorie classique du potentiel" , Sorbonne Univ. Centre Doc. Univ. , Paris (1959)

Comments

In axiomatic potential theory (cf. Potential theory, abstract) the equality of the best and the least harmonic majorant is connected to the domination principle (cf. Domination), see [a1], Chapt. 9.

References

[a1]	C. Constantinescu, A. Cornea, "Potential theory on harmonic spaces" , Springer (1972)