Pontryagin invariant
An invariant of framed constructions of surfaces with a given framing. Let 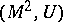 be a closed orientable surface with an
be a closed orientable surface with an  -dimensional framing
-dimensional framing 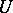 in
in 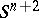 , i.e. a trivialization of the normal
, i.e. a trivialization of the normal  -dimensional vector bundle of the surface
-dimensional vector bundle of the surface 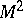 in
in 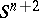 . Any element
. Any element 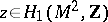 can be realized by a smoothly immersed circle with self-intersections which are only double points and transversal. Let some orientation of the circle
can be realized by a smoothly immersed circle with self-intersections which are only double points and transversal. Let some orientation of the circle 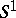 be fixed; let
be fixed; let 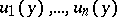 be orthogonal vectors from
be orthogonal vectors from 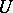 restricted to the point
restricted to the point 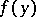 ,
, 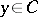 ; let
; let 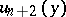 be the tangent vector to the curve
be the tangent vector to the curve 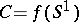 at the point
at the point 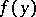 with respect to the chosen orientation of
with respect to the chosen orientation of 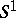 ; and let
; and let 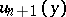 be the tangent vector to
be the tangent vector to 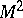 at
at 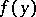 orthogonal to
orthogonal to 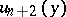 and oriented such that the sequence of vectors
and oriented such that the sequence of vectors 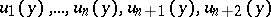 gives the standard orientation of the sphere
gives the standard orientation of the sphere  . The mapping
. The mapping 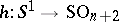 thus arising defines an element of the group
thus arising defines an element of the group 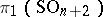 (which is isomorphic to
(which is isomorphic to 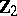 for
for 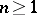 ). Let
). Let 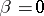 if
if 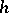 is homotopic to zero and
is homotopic to zero and 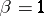 if
if 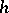 is not homotopic to zero. Let the value of the function
is not homotopic to zero. Let the value of the function  be equal to the sum modulo 2 of the number of double points of the curve
be equal to the sum modulo 2 of the number of double points of the curve 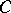 realizing the element
realizing the element  and the number
and the number 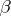 defined by
defined by 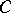 . Thus, a given value of
. Thus, a given value of 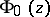 depends only on the homology class of
depends only on the homology class of  , and the function
, and the function 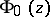 satisfies the following condition:
satisfies the following condition:
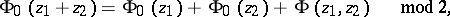 |
where 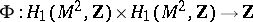 is the intersection form of one-dimensional homologies of the surface
is the intersection form of one-dimensional homologies of the surface 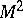 . The Arf-invariant of
. The Arf-invariant of 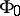 is called the Pontryagin invariant of the pair
is called the Pontryagin invariant of the pair 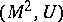 . The pair
. The pair 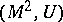 admits a framed surgery to the pair
admits a framed surgery to the pair 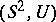 if and only if the Pontryagin invariant of the pair
if and only if the Pontryagin invariant of the pair 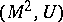 is zero (Pontryagin's theorem). The Pontryagin invariant can be realized by an
is zero (Pontryagin's theorem). The Pontryagin invariant can be realized by an 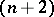 -dimensional framing of the torus,
-dimensional framing of the torus, 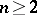 , and is the unique invariant of two-dimensional framed cobordism. The Pontryagin invariant defines an isomorphism
, and is the unique invariant of two-dimensional framed cobordism. The Pontryagin invariant defines an isomorphism  ,
, 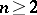 .
.
References
| [1] | L.S. Pontryagin, "Smooth manifolds and their applications in homology theory" , Moscow (1976) (In Russian) |
Comments
References
| [a1] | R.E. Stong, "Notes on cobordism theory" , Princeton Univ. Press (1968) |
| [a2] | J.W. Milnor, "Toplogy from the differentiable viewpoint" , Univ. Virginia Press (1966) |
Pontryagin invariant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pontryagin_invariant&oldid=15067