Pontryagin invariant

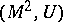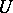An invariant of framed constructions of surfaces with a given framing. Let be a closed orientable surface with an -dimensional framing in 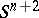, i.e. a trivialization of the normal -dimensional vector bundle of the surface 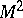in 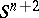. Any element 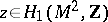can be realized by a smoothly immersed circle with self-intersections which are only double points and transversal. Let some orientation of the circle 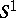be fixed; let 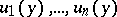be orthogonal vectors from 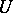restricted to the poin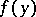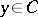t , ; let 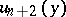be the tangent vector to the curve 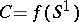at the point 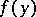with respect to the chosen orientation of 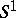; and let 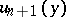be the tangent vector to 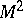at 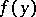orthogonal to 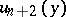and oriented such that the sequence of vectors 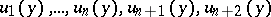gives the standard orientation of the sphere . 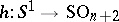The mapping thus arising defines an element of the group 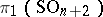(which is isomorphic to 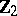for 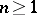). Let 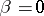if 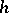is homotopic to zero and 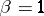if 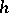is not homotopic to zero. 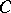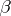Let the value of the function be equal to the sum modulo 2 of the number of double points of the curve realizing the element and the number defined by 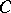. 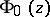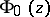Thus, a given value of depends only on the homology class of , and the function satisfies the following condition:

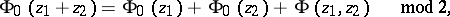where 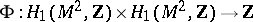is the intersection form of one-dimensional homologies of the surface 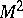. The Arf-invariant of 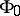is called the Pontryagin invariant of the pair 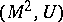. The pair 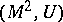admits a framed surgery to the pair 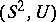if and only if the Pontryagin invariant of the pair 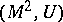is zero (Pontryagin's theorem). The Pontryagin invariant can be realized by an 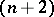-dimensional framing of the torus, 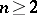, and is the unique invariant of two-dimensional framed cobordism. The Pontryagin invariant defines an isomorphism , .

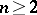References

[1]	L.S. Pontryagin, "Smooth manifolds and their applications in homology theory" , Moscow (1976) (In Russian)

References

[a1]	R.E. Stong, "Notes on cobordism theory" , Princeton Univ. Press (1968)
[a2]	J.W. Milnor, "Toplogy from the differentiable viewpoint" , Univ. Virginia Press (1966)