Retarded potentials, method of

Duhamel principle

A method for determining the solution to the homogeneous Cauchy problem for a (system of) inhomogeneous linear partial differential equation(s) in terms of the known solution to the homogeneous equation or system.

Consider the equation

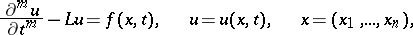(1)

where 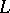is an arbitrary linear differential operator involving no derivatives with respect to 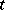of order higher than 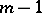. A particular solution 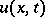of equation (1) (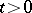) is looked for as a Duhamel integral:

(2)

where 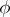is a (regular or generalized) solution of the homogeneous equation

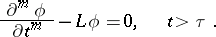If

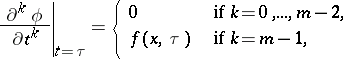then the function (2) obtained by superposition of the impulses is a solution to the Cauchy problem

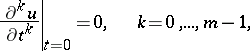(3)

for the inhomogeneous equation (1).

In the case of a system of ordinary differential equations, the method of retarded potentials is known as the method of variation of constants or the method of impulses. For ordinary linear differential equations of order ,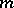

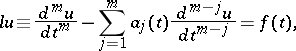(4)

the method proceeds as follows: if 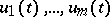is any fundamental system of solutions to the equation , then a solution 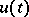to the inhomogeneous equation (4) is sought for in the form

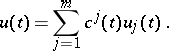The functions 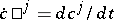, , 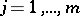are uniquely defined as the set of solutions to the system of algebraic equations

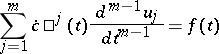with non-vanishing Wronskian.

If 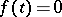for 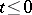, the solution of the homogeneous Cauchy problem (3) for equation (4) is usually called a normal reaction to the external load 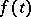. The function 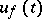can be expressed as a convolution or Duhamel integral:

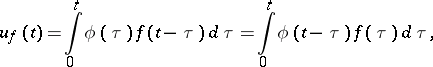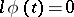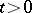where for and

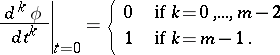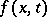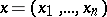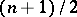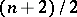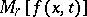Let , , be a function with continuous partial derivatives of order up to (if is odd) or (if is even), and let be the mean value of 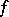on the sphere 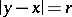with centre and radius . The function

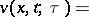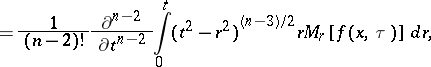which depends on the non-negative parameter 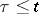, is a solution to the wave equation

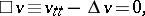satisfying the initial conditions

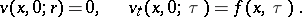The Duhamel integral

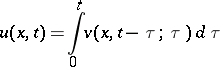(5)

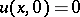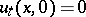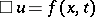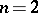is a solution to the homogeneous Cauchy problem , for the equation . If or 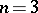, (5) implies

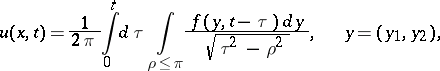or

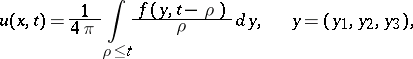(6)

where .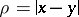

On the other hand, if , then

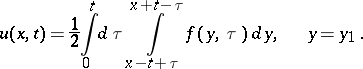The integral in (6) is known as a retarded potential with density .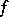

The method of retarded potentials (method of variation of parameters) is particularly simple and useful when applied to first-order linear systems of differential equations of the type

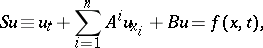(7)

where 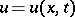is a 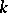-dimensional vector, 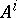and 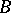are given 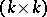-matrices and 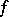is a given vector.

Suppose that the vector 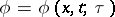, depending on a parameter 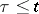, is a solution to the Cauchy problem

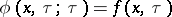for the homogeneous system 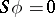. Then the vector

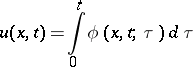(8)

is a solution to the inhomogeneous system (7) with initial condition

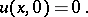(9)

The function corresponding to the inhomogeneous heat equation

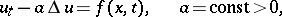(10)

has the form

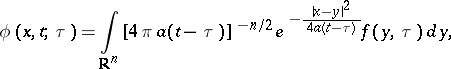(11)

where 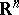is the Euclidean space. The solution 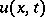of equation (10) with initial condition (9) is given by a Duhamel integral (3), with the function (11) as integrand.

The method of retarded potentials is also used to investigate mixed problems for partial differential equations of parabolic and hyperbolic types; it enables one to reduce the general problem to problems involving special initial and boundary functions.

For example, in the domain 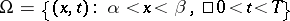, consider the partial differential equation

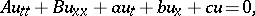(12)

where , ,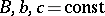

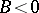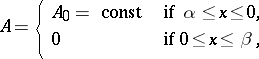which is hyperbolic if 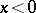and parabolic 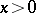if . If 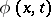is a continuous solution, differentiable at 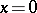, of the mixed problem

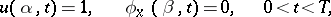for equation (12) in , then, according to the method of retarded potentials, the Duhamel integral

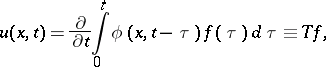(13)

with continuously-differentiable density 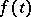, is a solution to the mixed problem

for equation (12) in .

Essentially, the Duhamel integral (13) is a formula representing a linear operator 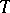which, given the boundary function 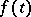, produces the solution 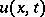. Duhamel's integral formula is valid not only for the operator 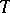of (13), but also for all linear operators 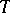satisfying the following conditions:

1) 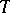is defined for all functions 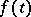vanishing for 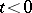, and maps 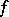to a function which also vanishes for .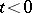

2)

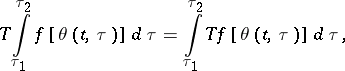where 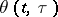is some function of 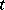and the parameter .

3) If 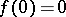and 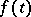is differentiable, then

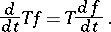4) If 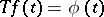, then for all ,

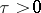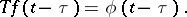References

[1]	A.V. Bitsadze, "Equations of mathematical physics" , MIR (1980) (Translated from Russian)
[2]	L. Bers, F. John, M. Schechter, "Partial differential equations" , Interscience (1964)
[3]	V.S. Vladimirov, "Equations of mathematical physics" , MIR (1984) (Translated from Russian)
[4]	R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , 2 , Interscience (1965) (Translated from German)
[5]	L.S. Pontryagin, "Ordinary differential equations" , Addison-Wesley (1962) (Translated from Russian)
[6]	A.N. Tikhonov, A.A. Samarskii, "Equations of mathematical physics" , Pergamon (1963) (Translated from Russian)