Levi-Civita connection
An affine connection on a Riemannian space  that is a Riemannian connection (that is, a connection with respect to which the metric tensor is covariantly constant) and has zero torsion. An affine connection on
that is a Riemannian connection (that is, a connection with respect to which the metric tensor is covariantly constant) and has zero torsion. An affine connection on  is determined uniquely by these conditions, hence every Riemannian space
is determined uniquely by these conditions, hence every Riemannian space  has a unique Levi-Civita connection. This concept first arose in 1917 with T. Levi-Civita [1] as the concept of parallel displacement of a vector in Riemannian geometry. The idea itself goes back to F. Minding, who in 1837 introduced the concept of the involute of a curve on a surface.
has a unique Levi-Civita connection. This concept first arose in 1917 with T. Levi-Civita [1] as the concept of parallel displacement of a vector in Riemannian geometry. The idea itself goes back to F. Minding, who in 1837 introduced the concept of the involute of a curve on a surface.
With respect to a local coordinate system in  , where
, where  , the Levi-Civita connection on
, the Levi-Civita connection on  is defined by the forms
is defined by the forms  , where
, where
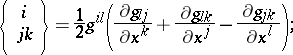 |
its curvature tensor 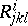 is defined by the formula
is defined by the formula
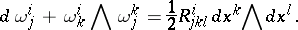 |
Let  ; then
; then
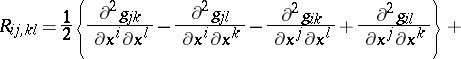 |
 |
thus:
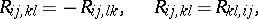 |
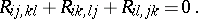 |
The curvature tensor of the Levi-Civita connection has 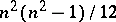 essential components, where
essential components, where  . For example, for
. For example, for 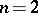 there is only one essential component:
there is only one essential component:  , where
, where  is the Gaussian curvature.
is the Gaussian curvature.
If a Riemannian space  is isometrically immersed in a Euclidean space
is isometrically immersed in a Euclidean space 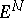 , then its Levi-Civita connection is characterized as follows: For two arbitrary vector fields
, then its Levi-Civita connection is characterized as follows: For two arbitrary vector fields  ,
,  on
on 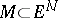 the covariant derivative
the covariant derivative 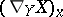 at a point
at a point 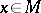 is the orthogonal projection on the tangent plane
is the orthogonal projection on the tangent plane  of the ordinary differential
of the ordinary differential 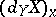 of the field
of the field 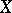 in
in 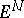 with respect to the vector
with respect to the vector 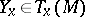 . In other words, the mapping of a neighbouring infinitely close tangent plane onto the original tangent plane is accomplished by orthogonal projection.
. In other words, the mapping of a neighbouring infinitely close tangent plane onto the original tangent plane is accomplished by orthogonal projection.
References
| [1] | T. Levi-Civita, "Nozione di parallelismo in una varietá qualunque e consequente specificazione geometrica della curvatura riemanniana" Rend. Circ. Math. Palermo , 42 (1917) pp. 173–205 |
| [2] | D. Gromoll, W. Klingenberg, W. Meyer, "Riemannsche Geometrie im Grossen" , Springer (1968) |
| [3] | P.K. [P.K. Rashevskii] Rashewski, "Riemannsche Geometrie und Tensoranalyse" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian) |
Comments
References
| [a1] | W. Klingenberg, "Riemannian geometry" , de Gruyter (1982) (Translated from German) |
Levi-Civita connection. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Levi-Civita_connection&oldid=14415