Skew-symmetric matrix

A square matrix 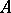over a field of characteristic 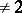such that 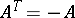. The rank of a skew-symmetric matrix is an even number. Any square matrix 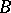over a field of characteristic 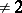is the sum of a symmetric and a skew-symmetric matrix:

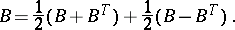The non-zero roots of the characteristic polynomial of a real skew-symmetric matrix are purely imaginary numbers. A real skew-symmetric matrix is similar to a matrix

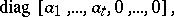where

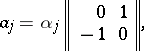with 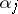real numbers, 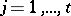. The Jordan form 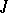of a complex skew-symmetric matrix possesses the following properties: 1) a Jordan cell 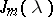with elementary divisor 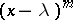, where 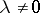, is repeated in 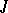as many times as is the cell 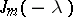; and 2) if 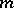is even, the Jordan cell 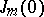with elementary divisor 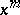is repeated in 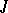an even number of times. Any complex Jordan matrix with the properties 1) and 2) is similar to some skew-symmetric matrix.

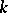The set of all skew-symmetric matrices of order over a field forms a Lie algebra over with respect to matrix addition and the commutator .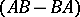

References

[1]	F.R. [F.R. Gantmakher] Gantmacher, "The theory of matrices" , 1 , Chelsea, reprint (1977) (Translated from Russian)

Comments

The Lie algebra of skew-symmetric matrices over a field 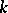of size 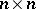is denoted by 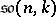. The complex Lie algebras (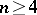) and 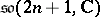(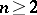) are simple of type 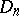and 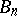, respectively.

References

[a1]	S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978) pp. Chapt. X