Generalized almost-periodic functions

Classes of functions that are various generalizations of almost-periodic functions. Each of them generalizes some aspects of Bohr and Bochner almost-periodic functions (cf. Bohr almost-periodic functions; Bochner almost-periodic functions). The following mathematical concepts (structures) occur in the definitions of Bohr and Bochner almost-periodicity: 1) the space of continuous functions defined on the whole line, regarded as a metric space with metric (distance)

(*)

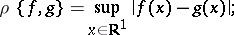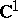2) a mapping of the line into the complex plane (a function); 3) the line 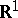as a group; and 4) the line as a topological space.

The existing generalizations of almost-periodic functions can conveniently be classified according to these structures.

1) If instead of continuity one requires the function 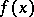, , 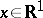to be measurable with summable 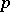-th power on each bounded interval, then one of the following three expressions can be taken for the distance:

the Stepanov distance:

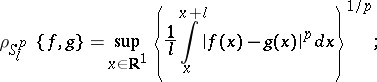the Weyl distance:

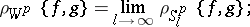the Besicovitch distance:

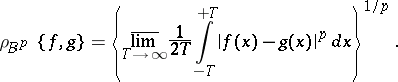Corresponding to these distances one has the generalized Stepanov, Weyl and Besicovitch almost-periodic functions (cf. Stepanov almost-periodic functions; Besicovitch almost-periodic functions; Weyl almost-periodic functions).

2) Suppose the line is mapped not into , but into a Banach space 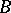. Such a mapping is called an abstract function. Suppose that the abstract functions are continuous and that the distance between them is defined by formula (*) with the modulus replaced by the norm. Then the definitions of Bohr and Bochner can be generalized and lead to the so-called abstract almost-periodic functions.

A further generalization can be obtained by replacing the Banach space by a topological vector space. In this case for every neighbourhood 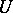of zero a real number 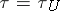is called an 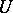-almost-period of 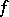whenever 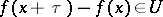for all .

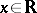If the norm-topology is replaced by the weak topology, then one obtains the so-called weak almost-periodic functions: A function 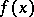, , 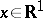, is called weakly almost-periodic if for any functional 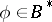, 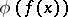is a numerical almost-periodic function.

3) Suppose that instead of the line 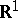one considers an arbitrary (not necessarily topological) group and a mapping 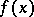, , 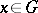of 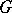into a topological vector space (in particular, into 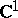). As a definition of almost-periodic functions it is convenient to take Bochner's definition: 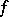is called an almost-periodic function on the group if the family of functions 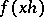, 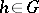(or, equivalently, the family 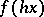), is conditionally compact with respect to uniform convergence on 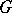(cf. Almost-periodic function on a group).

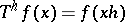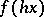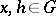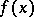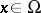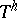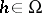4) In the definition of almost-periodic functions on a group, the important thing is not the group operation itself, but the displacement operator on functions: (or ), . Hence a further generalization of almost-periodic functions is obtained by generalizing the displacement operator. Let be an abstract space (not necessarily a group) and let , , be a function defined on . Linear operators , , are called generalized displacement operators if the following axioms are satisfied:

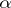) associativity: ;

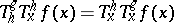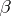) the existence of a neutral element, that is, an element 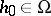such that , where 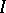is the identity operator.

A function 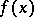, , 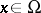is called almost-periodic relative to the family of generalized displacement operators 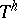if the family of functions ( 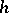a parameter) is conditionally compact with respect to uniform convergence on . It must be noted that the theory of such functions is still poorly developed, even relative to specific families of generalized displacement operators (see [1], [5]).

5) Let 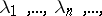be a finite or countable set of real numbers. Suppose that the line 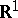is made into a topological vector space by defining a neighbourhood of the origin as a set of real numbers satisfying 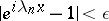, 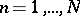(the numbers and 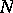are chosen arbitrarily and determine the neighbourhood). It turns out that the Bohr almost-periodic functions coincide with the functions that are uniformly continuous in this topology (for the numbers 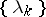one may take the Fourier indices of the function or an integral basis of them). Functions that are continuous in this topology provide another generalization of almost-periodic functions. These are the so-called Levitan 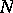-almost-periodic functions. The definition of 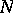-almost-periodic functions can be carried over in an obvious way to functions defined on an Abelian group (and, less obviously, to non-commutative groups).

The so-called asymptotic almost-periodic functions introduced by M. Fréchet (see [9], [10]) in connection with certain problems of ergodic theory do not fit particularly well into the above classification of generalized almost-periodic functions. 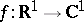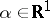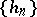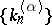A function is called an asymptotic almost-periodic function if for every and every arbitrary sequence of real numbers , with , there exists a subsequence of 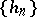for which 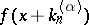converges uniformly for all .

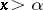References

[1]	B.M. Levitan, "Almost-periodic functions" , Moscow (1953) (In Russian)
[2]	A.S. Besicovitch, "Almost periodic functions" , Cambridge Univ. Press (1932)
[3]	L. Amerio, G. Prouse, "Almost-periodic functions and functional equations" , v. Nostrand-Reinhold (1971)
[4]	S. Bochner, "Abstrakte fastperiodische Funktionen" Acta Math. , 61 (1933) pp. 149–184
[5]	V.A. Marchenko, "Some questions in the theory of one-dimensional linear second-order differential operators" Trudy Moskov. Mat. Obshch. , 2 (1953) pp. 3–83 (In Russian)
[6]	B.Ya. Levin, "On the almost-periodic functions of Levitan" Ukrain. Mat. Zh. , 1 (1949) pp. 49–101 (In Russian)
[7]	A.S. Besicovitch, H. Bohr, "Almost periodicity and general trigonometric series" Acta Math. , 57 (1931) pp. 203–292
[8]	B.M. Levitan, V.V. Zhikov, "Almost-periodic functions and differential equations" , Cambridge Univ. Press (1982) (Translated from Russian)
[9]	M. Fréchet, "Les fonctions asymptotiquement presque-périodiques continues" C.R. Acad. Sci. Paris , 213 (1941) pp. 520–522
[10]	M. Fréchet, "Les transformations asymptotiquement presque périodiques discontinues et le lemme ergodique I" Proc. Roy. Soc. Edinburgh Sect. A , 63 (1950) pp. 61–68

Comments

More about this topic can be found in the articles Almost-periodic function and Almost-periodic function on a group.

In addition to the notion of weak almost-periodicity as defined above, there is another one which applies to complex-valued functions on a topological group 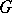(but can easily be generalized to functions with values in an arbitrary Banach space): A bounded continuous function 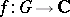is called weakly almost-periodic whenever the family of functions 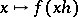, , 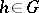is conditionally compact with respect to the weak topology in the space 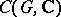of all bounded continuous functions from 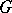to 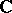. See [a3], [a1] and [a2]. In [a6] it is shown that these definitions are not equivalent for vector-valued functions.

For almost-periodicity with respect to (specific) families of generalized displacement operators, see [a5]. (In the above definition the sub-index in 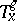denotes that the generalized displacement operator 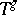is applied to a function of the variable . Thus, 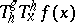is obtained by applying 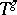to the function 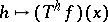.) Of the same flavour is the notion of an almost-periodic function on a transformation group: If a group 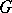acts continuously on a space 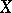, then a bounded continuous function 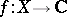is said to be (weakly) almost-periodic on the transformation group 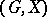whenever the family of functions , , 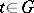is conditionally compact with respect to the uniform (respectively, weak) topology in the space 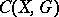. See e.g. [a4].

More about Levitan 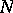-almost-periodic functions can be found in [8] and [a7].

References

[a1]	R.B. Burckel, "Weakly almost-periodic functions on semigroups" , Gordon & Breach (1970)
[a2]	K.S. de Leeuw, I. Glicksberg, "Almost periodic functions on semigroups" Acta Math. , 105 (1961) pp. 99–140
[a3]	W.F. Eberlein, "Abstract ergodic theorems and weak almost periodic functions" Trans. Amer. Math. Soc. , 67 (1949) pp. 217–240
[a4]	M.B. Landstadt, "On the Bohr compactification of a transformation group" Math. Z. , 127 (1972) pp. 167–178
[a5]	B.M. Levitan, "The application of generalized displacement operators to linear differential equations of the second order" Transl. Amer. Math. Soc. (1) , 10 (1950) pp. 408–451 Uspekhi Math. Nauk , 4 : 1(29) (1949) pp. 3–112
[a6]	P. Milnes, "On vector-valued weakly almost periodic functions" J. London Math. Soc. (2) , 22 (1980) pp. 467–472
[a7]	A. Reich, "Präkompakte Gruppen und Fastperiodicität" Math. Z. , 116 (1970) pp. 216–234