Conformal Euclidean space
A Riemannian space admitting a conformal mapping onto a Euclidean space. The curvature tensor of a conformal Euclidean space has the form
 | (*) |
where
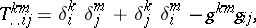 |
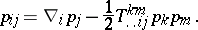 |
For  , every
, every  is a conformal Euclidean space. In order that a space with
is a conformal Euclidean space. In order that a space with  be a conformal Euclidean space, it is necessary and sufficient that there exist a tensor
be a conformal Euclidean space, it is necessary and sufficient that there exist a tensor  satisfying the conditions (*) and
satisfying the conditions (*) and  . Sometimes a conformal Euclidean space is called a Weyl space admitting a conformal mapping onto a Euclidean space (see [2]).
. Sometimes a conformal Euclidean space is called a Weyl space admitting a conformal mapping onto a Euclidean space (see [2]).
References
| [1] | J.A. Schouten, D.J. Struik, "Einführung in die neueren Methoden der Differentialgeometrie" , 2 , Noordhoff (1935) |
| [2] | A.P. Norden, "Spaces with an affine connection" , Nauka , Moscow-Leningrad (1976) (In Russian) |
Comments
The notion defined in the article above is also called a conformally Euclidean space. An alternative description of this notion is as follows. Let  be an
be an  -dimensional Riemannian space with Riemannian metric
-dimensional Riemannian space with Riemannian metric 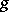 , Levi-Civita derivation (cf. Levi-Civita connection)
, Levi-Civita derivation (cf. Levi-Civita connection) 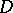 , curvature tensor
, curvature tensor  , Ricci transformation (cf. Ricci tensor)
, Ricci transformation (cf. Ricci tensor) 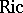 , and scalar curvature
, and scalar curvature  . Then the conformal curvature tensor
. Then the conformal curvature tensor 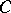 (Weyl's curvature tensor) is defined by
(Weyl's curvature tensor) is defined by
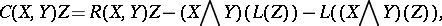 |
where
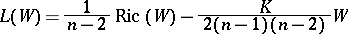 |
and
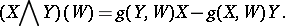 |
Then  locally admits a conformal mapping onto some open set of
locally admits a conformal mapping onto some open set of  if and only if
if and only if
1)  for
for  ; or
; or
2) 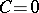 and
and  for
for 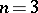 .
.
(See [a1] for example; for 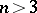 the "Codazzi equationCodazzi equation" for
the "Codazzi equationCodazzi equation" for 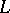 is satisfied automatically.) The coordinate expressions for the equations given above can be found in the book of J.A. Schouten [a2].
is satisfied automatically.) The coordinate expressions for the equations given above can be found in the book of J.A. Schouten [a2].
References
| [a1] | K. Yano, "The theory of Lie derivatives and its applications" , North-Holland (1957) |
| [a2] | J.A. Schouten, "Ricci-calculus. An introduction to tensor analysis and its geometrical applications" , Springer (1954) (Translated from German) |
Conformal Euclidean space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Conformal_Euclidean_space&oldid=14002