Finitely-generated group
A group  having a finite generating set
having a finite generating set 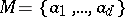 . It thus consists of all products
. It thus consists of all products 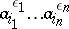 ,
, 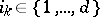 ,
,  . If
. If 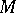 has
has 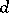 elements, then
elements, then 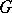 is said to be a
is said to be a 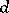 -generator group. Every generating set of a finitely-generated group contains a finite generating set. One-generator groups are said to be cyclic (they are isomorphic to either the additive group
-generator group. Every generating set of a finitely-generated group contains a finite generating set. One-generator groups are said to be cyclic (they are isomorphic to either the additive group 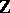 of integers, or the additive groups
of integers, or the additive groups  of residue classes of integers modulo
of residue classes of integers modulo  ,
, 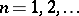 ).
).
The set of isomorphism classes of  -generator groups has the cardinality of the continuum. Every countable group can be isomorphically imbedded in a
-generator groups has the cardinality of the continuum. Every countable group can be isomorphically imbedded in a  -generator group; the imbedding group can be chosen to be simple and to be generated by an element of order 2 and one of order 3. Every countable
-generator group; the imbedding group can be chosen to be simple and to be generated by an element of order 2 and one of order 3. Every countable  -solvable group (cf. Solvable group) can be imbedded in a
-solvable group (cf. Solvable group) can be imbedded in a  -generator
-generator 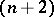 -solvable group. Every subgroup of finite index in a finitely-generated group is finitely generated. A finitely-generated group has only finitely many subgroups of given finite index. A finitely-generated group can be infinite and periodic; in fact, for every natural number
-solvable group. Every subgroup of finite index in a finitely-generated group is finitely generated. A finitely-generated group has only finitely many subgroups of given finite index. A finitely-generated group can be infinite and periodic; in fact, for every natural number  and every sufficiently large odd number
and every sufficiently large odd number  there exists an infinite
there exists an infinite 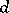 -generator group of exponent
-generator group of exponent  (see Burnside problem). A finitely-generated group can be isomorphic to a proper quotient group of itself; in this case it is called non-Hopfian (cf. Hopf group). There exist solvable non-Hopfian finitely-generated groups. A finitely-generated residually-finite group (see Residually-finite group) is Hopfian. Every finitely-generated group of matrices over a field is residually finite. There exist infinite finitely-generated, and even finitely-presented, groups that are simple (cf. Finitely-presented group).
(see Burnside problem). A finitely-generated group can be isomorphic to a proper quotient group of itself; in this case it is called non-Hopfian (cf. Hopf group). There exist solvable non-Hopfian finitely-generated groups. A finitely-generated residually-finite group (see Residually-finite group) is Hopfian. Every finitely-generated group of matrices over a field is residually finite. There exist infinite finitely-generated, and even finitely-presented, groups that are simple (cf. Finitely-presented group).
References
| [1] | M.I. Kargapolov, J.I. [Yu.I. Merzlyakov] Merzljakov, "Fundamentals of the theory of groups" , Springer (1979) (Translated from Russian) |
Comments
For references see also Finitely-presented group.
Finitely-generated group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Finitely-generated_group&oldid=13890