Translation-invariant metric
From Encyclopedia of Mathematics
invariant metric
A metric 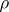 on a vector or linear space
on a vector or linear space 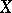 such that
such that 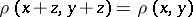 for all
for all 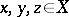 . A norm or an
. A norm or an 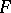 -norm,
-norm,  (cf. (the editional comments to) Universal space for a definition of this notion), defines a translation-invariant metric
(cf. (the editional comments to) Universal space for a definition of this notion), defines a translation-invariant metric 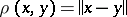 . If
. If 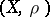 is a metric linear space, i.e. a vector space with a metric such that addition and scalar multiplication are continuous, then there is an invariant metric
is a metric linear space, i.e. a vector space with a metric such that addition and scalar multiplication are continuous, then there is an invariant metric 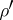 on
on 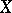 that is equivalent to the original one, [a2]. Two metrics
that is equivalent to the original one, [a2]. Two metrics 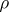 ,
, 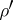 on
on 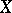 are equivalent if they induce the same topology.
are equivalent if they induce the same topology.
References
| [a1] | S. Rolewicz, "Metric linear spaces" , Reidel (1987) pp. §1.1 |
| [a2] | S. Kakutani, "Über die Metrisation der topologischen Gruppen" Proc. Imp. Acad. Tokyo , 12 (1936) pp. 82–84 |
How to Cite This Entry:
Translation-invariant metric. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Translation-invariant_metric&oldid=13810
Translation-invariant metric. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Translation-invariant_metric&oldid=13810