Tribonacci sequence
From Encyclopedia of Mathematics
An extension of the sequence of Fibonacci numbers having the form (with  ,
, 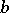 ,
,  given constants):
given constants):
 |
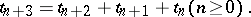 |
The concept was introduced by the fourteen-year-old student M. Feinberg in 1963 in [a1] for the case:  ,
, 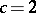 . The basic properties are introduced in [a5], [a3], [a4], [a2].
. The basic properties are introduced in [a5], [a3], [a4], [a2].
The Tribonacci sequence was generalized in [a6], [a7] to the form of two sequences:
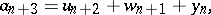 |
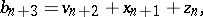 |
where 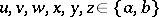 and each of the tuples
and each of the tuples 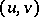 ,
, 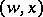 ,
, 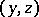 contains the two symbols
contains the two symbols  and
and 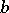 . There are eight different such schemes. An open problem (as of 2000) is the construction of an explicit formula for each of them.
. There are eight different such schemes. An open problem (as of 2000) is the construction of an explicit formula for each of them.
See also Tribonacci number.
References
| [a1] | M. Feinberg, "Fibonacci–Tribonacci" The Fibonacci Quart. , 1 : 3 (1963) pp. 71–74 |
| [a2] | C. Valavigi, "Properties of Tribonacci numbers" The Fibonacci Quart. , 10 : 3 (1972) pp. 231–246 |
| [a3] | A. Scott, T. Delaney, V. Hoggatt Jr., "The Tribonacci sequence" The Fibonacci Quart. , 15 : 3 (1977) pp. 193–200 |
| [a4] | A. Shannon, "Tribonacci numbers and Pascal's pyramid" The Fibonacci Quart. , 15 : 3 (1977) pp. 268; 275 |
| [a5] | I. Bruce, "A modified Tribonacci sequence" The Fibonacci Quart. , 22 : 3 (1984) pp. 244–246 |
| [a6] | K. Atanassov, J. Hlebarova, S. Mihov, "Recurrent formulas of the generalized Fibonacci and Tribonacci sequences" The Fibonacci Quart. , 30 : 1 (1992) pp. 77–79 |
| [a7] | J.-Z. Lee, J.-S. Lee, "Some properties of the generalization of the Fibonacci sequence" The Fibonacci Quart. , 25 : 2 (1987) pp. 111–117 |
How to Cite This Entry:
Tribonacci sequence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tribonacci_sequence&oldid=13626
Tribonacci sequence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tribonacci_sequence&oldid=13626
This article was adapted from an original article by Krassimir Atanassov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article