Lie algebra of an analytic group

Lie algebra of a Lie group 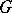defined over a field 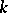that is complete with respect to a non-trivial absolute value

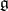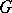The Lie algebra of regarded as local Lie group (cf. Lie group, local). Thus, as a vector space 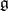is identified with the tangent space to 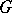at the point . The multiplication operation 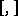in the Lie algebra can be defined in any of the following equivalent ways.

1) Let ad be the differential of the adjoint representation of the group 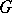(cf. Adjoint representation of a Lie group). Then 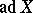, for any vector 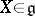, is a linear transformation of the space 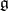and for any .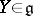

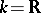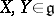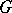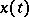2) Let , let be two tangent vectors to at and let and 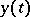be smooth curves in 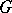for which 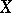and 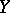are tangent vectors for 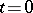. Then 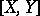is the tangent vector for 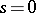to the curve 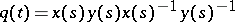, where 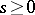and .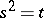

3) Let 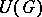be the associative 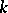-algebra of generalized functions on 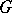with support at and with multiplication defined by the convolution . The space 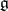is identified with the set of primitive elements (cf. Hopf algebra) of the bi-algebra 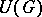, and for any 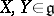the vector 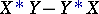also lies in 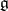. Then .

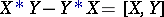4) Let 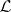be the vector space of all vector fields on 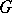that are invariant with respect to left translation by elements of 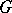. The correspondence between the vector field and its value at the point 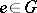is an isomorphism of the vector spaces 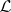and 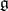. On the other hand, to any vector field 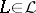corresponds a left-invariant derivation of the 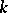-algebra 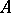of analytic functions on 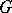by means of the formula 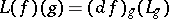for any 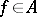, , 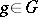and this correspondence is an isomorphism of the space 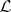to the vector space of all left-invariant derivations of 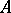. For any 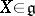, let 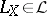denote the left-invariant vector field for which 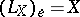. If 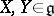, then the product 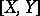can be defined as the vector of 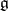for which the field 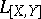specifies the derivation 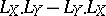of the algebra .

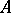Example. Let 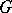be the analytic group of all non-singular matrices of order with coefficients in 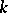. Then the tangent space 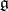to 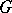at the identity is identified with the space of all matrices of order with coefficients in 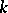, and a Lie algebra structure on 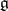is defined by the formula .

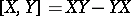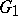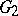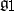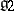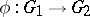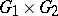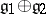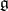The correspondence between an analytic group and its Lie algebra has important functorial properties and significantly reduces the study of analytic groups to the study of their Lie algebras. Namely, let and be analytic groups with Lie algebras and and let be an analytic homomorphism. Then is a homomorphism of Lie algebras. The Lie algebra of the analytic group is isomorphic to . If is the Lie algebra of an analytic group 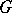, 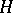is a Lie subgroup of 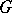(see Lie group) and 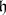is the Lie algebra of the analytic group 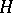, then 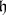is a subalgebra of 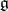, while if 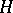is normal, then 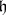is an ideal of 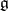. Suppose that the characteristic of 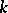is zero. The Lie algebra of an intersection of Lie subgroups coincides with the intersection of their Lie algebras. The Lie algebra of the kernel of a homomorphism 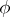of analytic groups is the kernel of the homomorphism 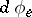of their Lie algebras. The Lie algebra of the quotient group 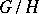, where 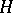is an analytic normal subgroup of 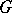, is the quotient algebra of the Lie algebra of 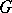with respect to the ideal corresponding to 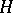. 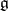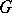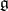If is the Lie algebra of an analytic group and is a subalgebra of , then there is a unique connected Lie subgroup 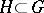with Lie algebra 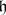; 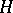need not be closed in 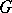. The Lie algebra of an analytic group is solvable (nilpotent, semi-simple) if and only if the group itself is solvable (nilpotent, semi-simple).

This connection between the categories of analytic groups and Lie algebras is not, however, an equivalence of these categories, in contrast to the case of local Lie groups. Namely, non-isomorphic analytic groups can have isomorphic Lie algebras. Analytic groups with isomorphic Lie algebras are said to be locally isomorphic. In the case of a field 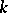of characteristic zero, to each finite-dimensional Lie algebra over 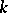corresponds a class of locally isomorphic analytic groups. Suppose that 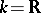or 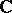. Among all locally isomorphic analytic groups there is a connected simply-connected group, which is unique up to isomorphism; the category of analytic groups of this type is equivalent to the category of finite-dimensional Lie algebras over 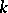. In particular, every homomorphism of Lie algebras is induced by an analytic homomorphism of the corresponding connected simply-connected analytic groups. Any connected Lie group that is locally isomorphic to a given connected simply-connected Lie group 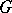has the form 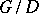, where 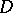is a discrete normal subgroup lying in the centre of .

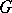References

[1]	N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French)
[2]	L.S. Pontryagin, "Topological groups" , Princeton Univ. Press (1958) (Translated from Russian)
[3]	J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) (Translated from French)
[4]	A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian)
[5]	C. Chevalley, "Theory of Lie groups" , 1 , Princeton Univ. Press (1946)

Comments

The unique connected simply-connected Lie group ove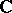r or 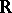that is locally isomorphic to a connected Lie group 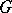is called the covering group of 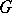. Existence and uniqueness are due to L.S. Pontryagin (1966).

So, the global structure of a Lie group 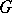is as follows. 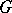consists of a discrete number of connected components. The component 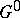containing the identity is normal in 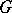(and both open and closed). Thus 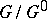is a discrete group. Often, particularly when 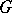is compact, 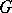is a semi-direct product: 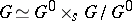. Finally, there exists a simply-connected connected covering group of 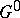with a projection 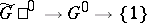of which the kernel is discrete and contained in the centre of .

References

[a1]	V.S. Varadarajan, "Lie groups, Lie algebras and their representations" , Prentice-Hall (1974)