Contingency equation

A relation

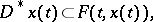where 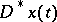is the contingency of a vector function 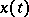, i.e. the set of all partial limits of the ratio

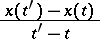as , while 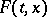is a given non-empty set in 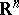, depending on 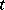and (cf. [1], [2]). If 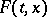is a bounded closed convex set that is upper semi-continuous relative to the inclusion function of the point 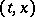, the contingency equation is equivalent to the paratingency equation (defined analogously to the contingency equation, but using the ratio

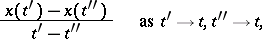cf. [3]) and the differential inclusion

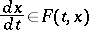(cf. [4]). The properties of a contingency equation are similar to those of a differential inclusion.

References

[1]	A. Marchaud, "Sur les champs de demi-cônes et les équations différentielle du premier ordre" Bull. Soc. Math. France , 62 (1934) pp. 1–38
[2]	E.A. Barbashin, Yu.I. Alimov, "On the theory of relay differential equations" Izv. Vysshikh Uchebn. Zaved. Mat. : 1 (1962) pp. 3–13 (In Russian)
[3]	S.K. Zaremba, "Sur les équations au paratingent" Bull. Sci. Math. (2) , 60 : 5 (1936) pp. 139–160
[4]	T. Waźewski, "Sur une condition équivalente à l'équation au contingent" Bull. Acad. Sci. Polon. Sci. Ser. Math. , 9 : 12 (1961) pp. 865–867