Gauss kernel

The -dimensional Gauss (or Weierstrass) kernel

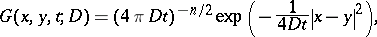with 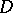a positive constant, 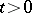, , 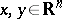is the fundamental solution of the -dimensional heat equation 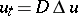. Moreover, this kernel is an approximate identity in that the Gauss–Weierstrass singular integral at the function ,

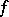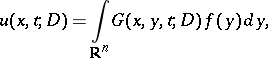satisfies 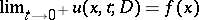almost everywhere, for example, whenever 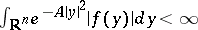for some 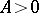; see [a4]. Thus 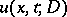is a solution of the heat equation for 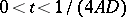, having the initial "temperature" .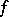

In the theory of Markov processes (cf. Markov process) the Gauss kernel gives the transition probability density of the Wiener–Lévy process (or of Brownian motion). The semi-group property of the Gauss kernel

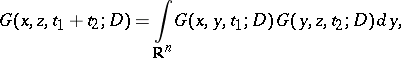is essential here.

References

[a1]	P. Butzer, R. Nessel, "Fourier analysis and approximation" , I , Birkhäuser (1971)
[a2]	R. Courant, D. Hilbert, "Methods of mathematical physics" , II , Wiley (1962)
[a3]	W. Feller, "An introduction to probability theory and its applications" , 2 , Springer (1976) (Edition: Second)
[a4]	E.C. Titchmarsh, "Introduction to the theory of Fourier integrals" , Clarendon Press (1937)
[a5]	K. Weierstrass, "Ueber die analytische Darstellbarkeit sogenannter willkurlichen Functionen reeler Argumente" Berliner Sitzungsberichte (1985) pp. 633–639; 789–805