Sum function of a function

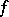
The function of 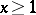that denotes the sum of the values 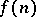of the function 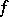on the set of natural numbers 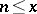, . Sum functions are one of the basic means of expressing various properties of sequences of numbers.

Examples of sum functions: the number of prime numbers 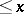; 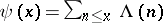— the Chebyshev function; the number of divisors of all 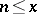, etc. (see [1], [2]).

The basic problem is to find as accurate as possible an expression of the sum function, and for a sum function which does not have asymptotics, to find the best estimate of its modulus for large values of .

The Cauchy integral theorem and Dirichlet series of the form

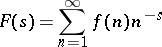form the basis of the analytic methods of studying sum functions. If such a series converges absolutely for , then for a non-integer , and 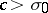, the identity

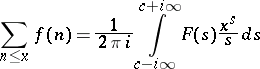holds; a corresponding estimate of the sum function of 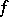is obtained from this by analytic continuation of by shifting the integration path to the left to a certain 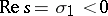and estimating the integral along the new path. If 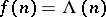, for example, the integration can be shifted to 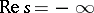, which gives the Riemann–von Mangoldt formula for 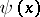. Of the common applications of the method, the following theorem is known.

Assumptions:

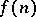, are complex numbers, , , 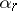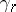are real numbers, , are positive numbers, 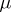and are integers 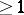, is the gamma-function, and .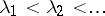

1) For any , ;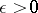

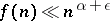2) the function

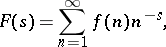defined for 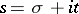, , 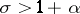is meromorphic in the whole plane, and has a finite number of poles in the strip ;

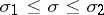3) the series 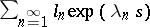converges absolutely when ;

4) for ,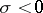

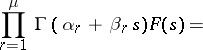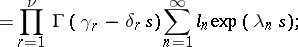5) ;

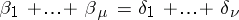6) if one assumes that

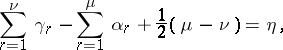then .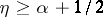

For a fixed strip 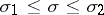there is a constant 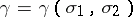such that for 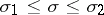and large 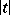the estimate holds.

Conclusion.

For any ,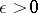

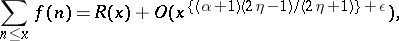where 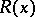is the sum of the residues of the function 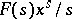over all its poles in the strip

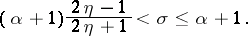References

[1]	E.C. Titchmarsh, "The theory of the Riemann zeta-function" , Clarendon Press (1951)
[2]	L.-K. Hua, "Abschätzungen von Exponentialsummen und ihre Anwendung in der Zahlentheorie" , Enzyklopaedie der Mathematischen Wissenschaften mit Einschluss ihrer Anwendungen , 1 : 2 (1959) (Heft 13, Teil 1)

Comments

The Riemann–von Mangoldt formula, or von Mangoldt formula, for 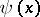, , 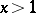is

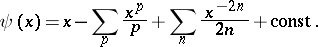This is von Mangoldt's reformulation of Riemann's main formula

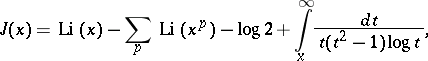wher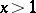e , the 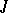-function is

and 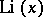is the logarithmic integral

References

[a1]	H.M. Edwards, "Riemann's zeta function" , Acad. Press (1974) pp. Chapt. 3