Multi-dimensional variational problem

variational problem involving partial derivatives

A problem in the calculus of variations (cf. Variational calculus) in which it is required to determine an extremum of a functional depending on a function of several independent variables. Ordinary variational problems, in which functionals of functions of one independent variable are considered, may be called one-dimensional variational problems, in this sense.

An example of a two-dimensional variational problem is the problem of determining a function of two independent variables, 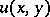, which, together with its first-order partial derivatives, is continuous and yields an extremum of the functional

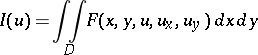(1)

under the boundary condition

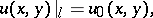(2)

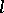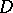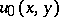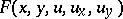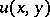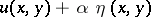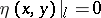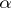where is a closed contour bounding a domain , is a given function and is a twice continuously-differentiable function jointly in its arguments. Let be a solution of the problem (1), (2). Substitution of a comparison function , where and is a numerical parameter, into (1), differentiation with respect to 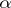and equating 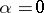, gives the following expression for the first variation of the functional:

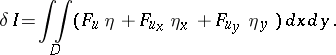(3)

If 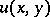has continuous second-order derivatives, then it is easy to show that a necessary condition for 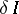to vanish is:

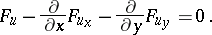(4)

Equation (4) is called the Euler–Ostrogradski equation (sometimes the Ostrogradski equation). This equation must be satisfied by a function which gives an extremum of (1) under the boundary conditions (2). The Euler–Ostrogradski equation is analogous to the Euler equation for one-dimensional problems. In expanded form, (4) is a second-order partial differential equation.

In the case of a triple integral and a function depending on three independent variables, the Euler–Ostrogradski equation takes the form:

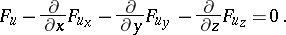The following condition is an analogue of the Legendre condition. In order that 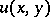gives at least a weak extremum of (1) it is necessary that at each interior point of ,

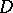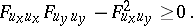For a minimum necessarily 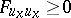, and for a maximum .

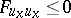Discontinuous multi-dimensional variational problems have also been considered (see [4]).

References

[1]	R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , 2 , Interscience (1965) (Translated from German)
[2]	V.I. Smirnov, "A course of higher mathematics" , 4 , Addison-Wesley (1964) (Translated from Russian)
[3]	N.I. Akhiezer, "The calculus of variations" , Blaisdell (1962) (Translated from Russian)
[4]	M.K. Kerimov, "On two-dimensional continuous problems of variational calculus" Trudy Tbilis. Mat. Inst. Akad. Nauk GruzSSR , 18 (1951) pp. 209–219 (In Russian)