Extension of a Lie algebra

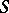with kernel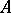

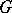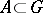A Lie algebra with an epimorphism whose kernel is an ideal . This is equivalent to specifying an exact sequence

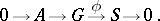The extension is said to split if there is a subalgebra 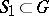such that 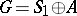(direct sum of modules). Then 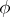induces an isomorphism 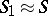, and defines an action of the algebra 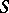on 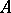by derivations. Conversely, any homomorphism 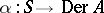, where 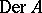is the algebra of derivations of 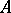, uniquely determines a split extension 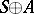with multiplication given by

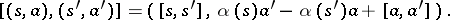For finite-dimensional Lie algebras over a field of characteristic 0, Lévy's theorem holds: If is semi-simple, then every extension of 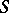splits.

Of all non-split extensions, the Abelian ones have been studied most, i.e. the extensions with an Abelian kernel 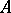. In this case the action of 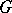on 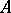induces an action of 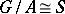on 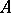, that is, 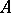is an 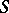-module. For Lie algebras over a field, every Abelian extension of 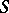with as kernel an 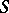-module 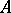has the form 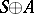with multiplication given by

where 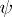is some linear mapping 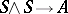. The Jacobi identity is equivalent to the fact that 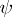is a two-dimensional cocycle (or -cocycle, see Cohomology of Lie algebras). The extensions determined by cohomologous cocycles are equivalent in a natural sense. In particular, an extension is split if and only if 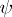is cohomologous to zero. Thus, the Abelian extensions of an algebra 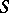with kernel 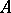are described by the cohomology group 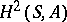. The study of extensions with solvable kernel reduces to the case of Abelian extensions.

References

[1]	N. Jacobson, "Lie algebras" , Interscience (1962) ((also: Dover, reprint, 1979))