Modular curve
A complete algebraic curve 
uniformized by a subgroup 
of finite index in the modular group 
; more precisely, a modular curve is a complete algebraic curve obtained from a quotient space 
, where 
is the upper half-plane, together with a finite number of parabolic points (the equivalence classes relative to 
of the rational points of the boundary of 
). The best known examples of subgroups 
of finite index in 
are the congruence subgroups containing a principal congruence subgroup 
of level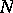 
for some integer 
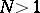, represented by the matrices
 |
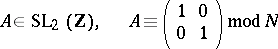(see Modular group). The least such 
is called the level of the subgroup 
. In particular, the subgroup 
represented by matrices which are congruent 
to upper-triangular matrices has level 
. Corresponding to each subgroup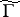 
of finite index there is a covering of the modular curve 
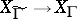, which ramifies only over the images of the points 
, 
, 
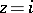. For a congruence subgroup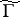 
the ramification of this covering allows one to determine the genus of 
and to prove the existence of subgroups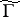 
of finite index in 
which are not congruence subgroups (see [4], Vol. 2, [2]). The genus of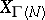 
is 
for 
and equals
 |
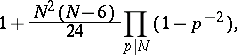a prime number, for 
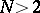. A modular curve is always defined over an algebraic number field (usually over 
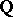or a cyclic extension of it). The rational functions on a modular curve lift to modular functions (of a higher level) and form a field; the automorphisms of this field have been studied (see [2]). A holomorphic differential form on a modular curve 
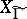is given on 
by a differential 
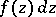(where 
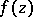is a holomorphic function) which is invariant under the transformations 
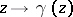of 
; here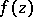 
is a cusp form of weight 2 relative to 
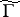. The zeta-function of a modular curve is a product of the Mellin transforms (cf. Mellin transform) of modular forms and, consequently, has a meromorphic continuation and satisfies a functional equation. This fact serves as the point of departure for the Langlands–Weil theory on the relationship between modular forms and Dirichlet series (see [7], [8]). In particular, there is a hypothesis that each elliptic curve over 
(with conductor 
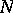) can be uniformized by modular functions of level 
. The homology of a modular curve is connected with modular symbols, which allows one to investigate the arithmetic of the values of the zeta-function of a modular curve in the centre of the critical strip and to construct the 
-adic zeta-function of a modular curve (see [1]).
A modular curve parametrizes a family of elliptic curves, being their moduli variety (see [7], Vol. 2). In particular, for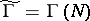 
a point 
of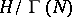 
is in one-to-one correspondence with a pair consisting of an elliptic curve 
(analytically equivalent to a complex torus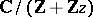 
) and a point of order 
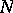on 
(the image of 
).
Over each modular curve 
there is a natural algebraic fibre bundle 
of elliptic curves if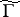 
does not contain 
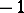, compactified by degenerate curves above the parabolic points of 
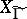. Powers 
, where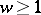 
is an integer, are called Kuga varieties (see [3], [5]). The zeta- functions of 
are related to the Mellin transforms of modular forms, and their homology to the periods of modular forms (see [3], [7]).
The rational points on a modular curve correspond to elliptic curves having rational points of finite order (or rational subgroups of points); their description (see [6]) made it possible to solve the problem of determining the possible torsion subgroups of elliptic curves over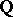 
.
The investigation of the geometry and arithmetic of modular curves is based on the use of groups of automorphisms of the projective limit of the curves 
with respect to decreasing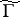 
, which (in essence) coincides with the group 
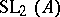over the ring 
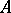of rational adèles. On each modular curve 
this gives a non-trivial ring of correspondences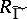 
(a Hecke ring), which has applications in the theory of modular forms (cf. Modular form, [3]).
References
| [1] | Yu.I. Manin, "Parabolic points and zeta-functions of modular curves" Math. USSR Izv. , 6 : 1 (1972) pp. 19–64 Izv. Akad. Nauk SSSR Ser. Mat. , 36 : 1 (1972) pp. 19–66 |
| [2] | G. Shimura, "Introduction to the arithmetic theory of automorphic functions" , Math. Soc. Japan (1971) |
| [3] | V.V. [V.V. Shokurov] Šokurov, "Holomorphic differential forms of higher degree on Kuga's modular varieties" Math. USSR Sb. , 30 : 1 (1976) pp. 119–142 Mat. Sb. , 101 : 1 (1976) pp. 131–157 |
| [4] | F. Klein, R. Fricke, "Vorlesungen über die Theorie der elliptischen Modulfunktionen" , 1–2 , Teubner (1890–1892) |
| [5] | M. Kuga, G. Shimura, "On the zeta function of a fibre variety whose fibres are abelian varieties" Ann. of Math. , 82 (1965) pp. 478–539 |
| [6] | B. Mazur, J.-P. Serre, "Points rationnels des courbes modulaires 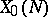 (d'après A. Ogg)" , Sem. Bourbaki 1974/1975 , Lect. notes in math. , 514 , Springer (1976) pp. 238–255 |
| [7] | J.-P. Serre (ed.) P. Deligne (ed.) W. Kuyk (ed.) , Modular functions of one variable. 1–6 , Lect. notes in math. , 320; 349; 350; 476; 601; 627 , Springer (1973–1977) |
| [8] | A. Weil, "Ueber die Bestimmung Dirichletscher Reihen durch Funktionalgleichungen" Math. Ann. , 168 (1967) pp. 149–156 |
Comments
References
| [a1] | N.M. Katz, B. Mazur, "Arithmetic moduli of elliptic curves" , Princeton Univ. Press (1985) |
Modular curve. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Modular_curve&oldid=13202